~双極子モーメント~
問題
図に示すように真空中に置かれた双極子によるP点の電位\(V\)は、
\[V=\frac{1}{4\pi \varepsilon_0}\frac{(\mu \cdot r)}{r^3}\]
で与えられるが、次の問に答えよ。ただし、\(\varepsilon_0\)は真空の誘電率、\(\mu\)は双極子モーメントのベクトル、\(r\)は動径ベクトルである。
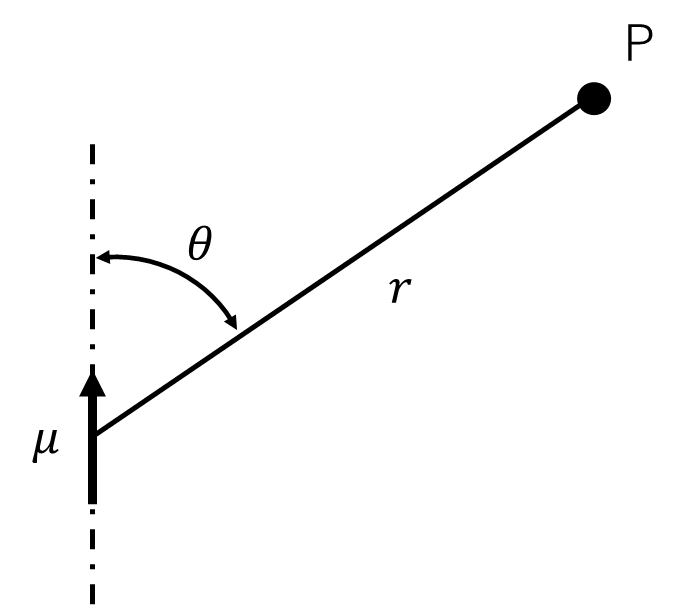
(1)\(\mu\)と\(r\)のなす角を\(\theta\)とするとき、双極子の作るP点の電界の球座標における\(r\)、\(\theta\)、\(\varphi\)方向成分を求めよ。
(2)双極子モーメント\(\mu\)の双極子が下図のように、原点Oの左右に一直線上に等間隔\(a\)で無限に並んでいるとき、これらすべての双極子による原点Oにおける電界\(E_d\)の大きさを求めよ。
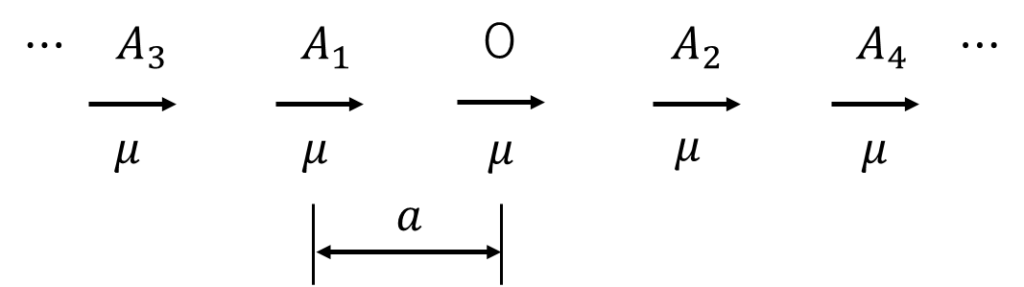
ただし
\[\sum^{\infty}_{n=1}{\frac{1}{n^3}}\fallingdotseq 1.2\]
(3)\(\mu\)が外部電界\(E\)により、これと同じ方向に生じたものとするとき、(2)の場合の原点における内部電界\(E_i\)を求めよ。ただし、分極率を\(\alpha\)とする。
解答
(1)双極子の作るP点の電界の球座標における\(r\)、\(\theta\)、\(\varphi\)方向成分
\(r\)方向成分
\[\frac{\mu \cos{\theta}}{2\pi \varepsilon_0 r^3}\]
\(\theta\)方向成分
\[\frac{\mu \sin{\theta}}{4\pi \varepsilon_0 r^3}\]
\(\varphi\)方向成分
\[0\]
(2)原点Oにおける電界\(E_o\)の大きさ
\[E_o=\frac{1.2\mu}{\pi \varepsilon_0 a^3}\]
(3)\(\mu\)が同じ方向に生じたものとするときの(2)の場合の原点における内部電界\(E_i\)
\[E_i=\frac{\pi \varepsilon_0 a^3}{\pi \varepsilon_0 a^3-1.2\alpha}\]
解説
問題の図を球座標に示す。
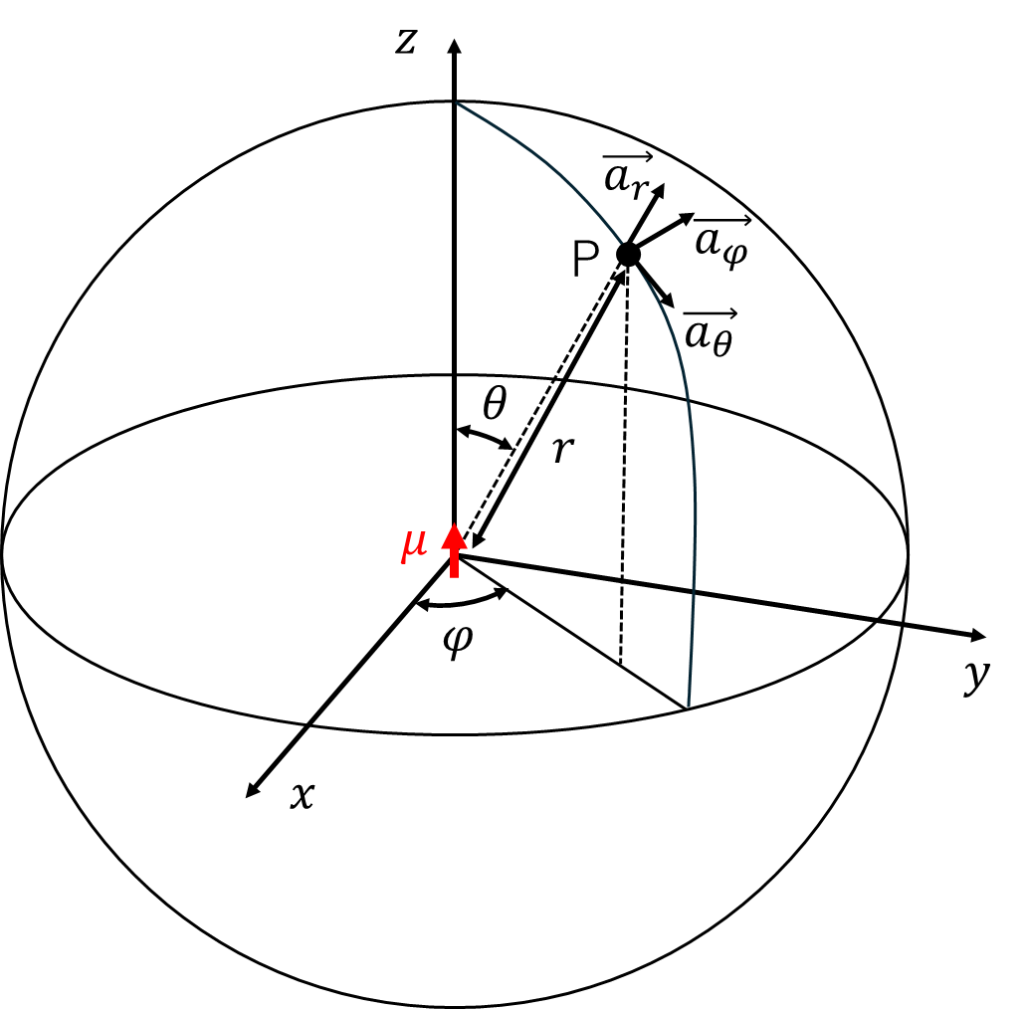
\(r\)は半径、\(\varphi\)は方位角、\(\theta\)は仰角である。ここで、\(\vec{a_r}\)、\(\vec{a_{\varphi}}\)、\(\vec{a_{\theta}}\)はそれぞれの成分の単位ベクトルである。
(1)双極子の作るP点の電界の球座標における\(r\)、\(\theta\)、\(\varphi\)方向成分
電界\(E\)は変位\(x\)による電位\(V\)の傾きである。よって、以下の式が成り立つ。
\[E=-\frac{\partial V}{\partial x}\]
負号がつくのは、電界は電位が減少する方向に進むためである。
これを、それぞれの成分に置き換えて考える。
問題で与えられた\(V\)において、内積\(\vec{\mu} \cdot \vec{r}=\mu r\cos{\theta}\)である。
\[V=\frac{1}{4\pi \varepsilon_0}\frac{(\mu \cdot r)}{r^3}=\frac{\mu \cos{\theta}}{4\pi \varepsilon_0 r^2}\]
\(r\)方向成分
\(r\)方向成分の電界を\(E_r\)とすると、
\[E_r=-\frac{\partial V}{\partial r}\]
で与えられる。\(r\)の微小変化はそのまま距離の変化と一致することから、係数は必要ない。
\[E_r=-\frac{\mu \cos{\theta}}{4\pi \varepsilon_0}\frac{d}{d r}r^{-2}=\frac{\mu \cos{\theta}}{2\pi \varepsilon_0 r^3}\]
\(\theta\)方向成分
\(\theta\)方向成分の電界を\(E_{\theta}\)とすると、
\[E_{\theta}=-\frac{1}{r}\frac{\partial V}{\partial \theta}\]
で与えられる。\(\theta\)の微小変化\(d\theta\)による距離変化は\(rd\theta\)となるため、\(\frac{1}{r}\)という補正が必要となる。
\[E_{\theta}=-\frac{\mu}{4\pi \varepsilon_0 r^3}\frac{d}{d \theta}\cos{\theta}=\frac{\mu \sin{\theta}}{4\pi \varepsilon_0 r^3}\]
\(\varphi\)方向成分
\(\varphi\)方向成分の電界を\(E_{\varphi}\)とすると、
\[E_{\varphi}=-\frac{1}{r\sin{\theta}}\frac{\partial V}{\partial \varphi}\]
で与えられる。\(\varphi\)の微小変化\(d\varphi\)による距離変化は\(r\sin{\theta}d\varphi\)となるため、\(\frac{1}{r\sin{\theta}}\)という補正が必要となる。
ただし、\(V\)は\(\varphi\)に無関係であることから、\(\varphi\)の変化による電位の勾配は\(0\)である。よって
\[E_{\varphi}=0\]
(2)原点Oにおける電界\(E_o\)の大きさ

\[E_r=\frac{\mu \cos{\theta}}{2\pi \varepsilon_0 r^3}\]
この式において、\(\theta=0\)、\(r\)を\(a\)に置き換えて計算すればよい。
原点からみて片側の双極子による電界は以下のようになる。
\[\frac{\mu}{2\pi \varepsilon_0 a^3}+\frac{\mu}{2\pi \varepsilon_0 (2a)^3}+\frac{\mu}{2\pi \varepsilon_0 (3a)^3}+\cdots\]
\[=\frac{\mu}{2\pi \varepsilon_0 a^3}\left(\frac{1}{1^3}+\frac{1}{2^3}+\frac{1}{3^3}+\cdots\right)=\frac{\mu}{2\pi \varepsilon_0 a^3}\sum^{\infty}_{n=1}{\frac{1}{n^3}}\]
これが対称になっていることから、2倍となる。
\[E_o=\frac{\mu}{\pi \varepsilon_0 a^3}\sum^{\infty}_{n=1}{\frac{1}{n^3}}\]
\(\sum^{\infty}_{n=1}{\frac{1}{n^3}}\)はリーマンゼータ関数といわれ、\(\zeta(3)\)とも表記される。\(\zeta(3)\fallingdotseq 1.2\)より
\[E_o=\frac{1.2\mu}{\pi \varepsilon_0 a^3}\]
(3)\(\mu\)が同じ方向に生じたものとするときの(2)の場合の原点における内部電界\(E_i\)
内部電界\(E_i\)は、外部電界\(E\)と\(E_o\)との和となる。
\[E_i=E+E_o=E+\frac{1.2\mu}{\pi \varepsilon_0 a^3}\]
\(\mu=\alpha E_i\)より、
\[E_i=E+\frac{1.2\alpha E_i}{\pi \varepsilon_0 a^3}\to E_i\left(1-\frac{1.2\alpha}{\pi \varepsilon_0 a^3}\right)=E\]
よって
\[E_i=\frac{\pi \varepsilon_0 a^3}{\pi \varepsilon_0 a^3-1.2\alpha}\]
外部電場\(E\)をかけると、物質中の正負の電荷がわずかに引き離され、この電荷のずれによって双極子モーメント\(\mu\)が生じる。
出典
昭和54年度第一種電気主任技術者筆記試験理論問3



コメント