電線3本のうち1本が地面とつながっちゃった!って事故です。
どう解析していくのでしょうか?
どうして一線地絡が起こるの?
雷大国、日本。とんでもなく大きい雷電流がながれることで、電気製品を破壊してしまいます。
送電線も例外ではありません。
雷によるアークにより、一線が地面とつながってしまいます。
送電系統での事故は、圧倒的に一線地絡が多いです。
モデル化した系統より
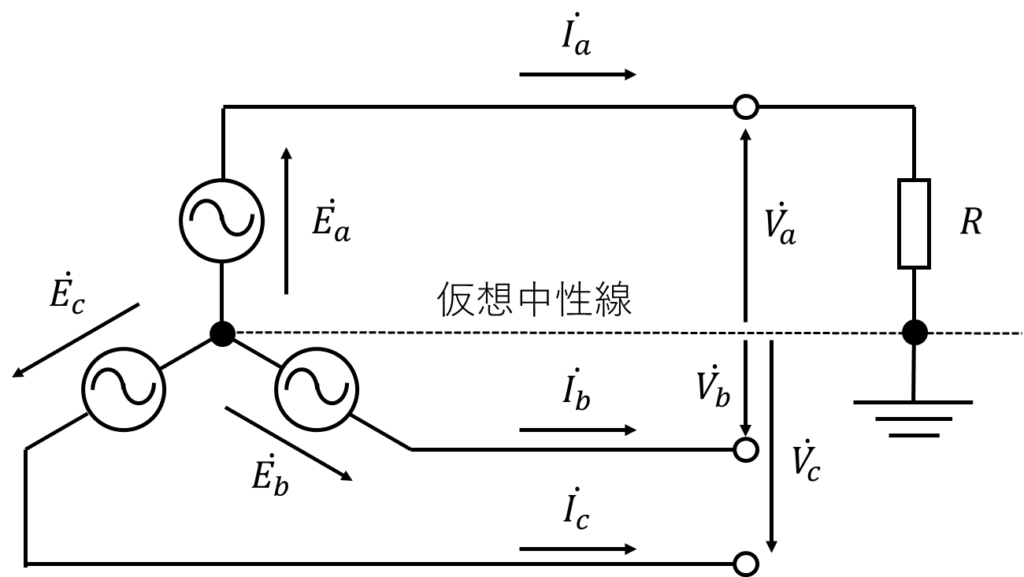
図の系統を用いて解説します。
a相にて、抵抗Rを介して地絡しています。
地絡電流は\(\dot{I_a}\)です。
これを正相電圧、対称分インピーダンスで表します。
故障条件を求める
故障条件を書き出していきます。
b相、c相は解放されていることから、
\[\dot{I_b}=\dot{I_c}=0\]
a相電圧はオームの法則より
\[\dot{V_a}=\dot{I_a} R\]
この2つの式を対称分へ変換していきます。
対称分へ変換
電流に関する式
\(\dot{I_b}\)、\(\dot{I_c}\)を変換します。
\[\dot{I_b}=\dot{I_0}+a^2\dot{I_1}+a\dot{I_2}\]
\[\dot{I_c}=\dot{I_0}+a\dot{I_1}+a^2\dot{I_2}\]
\(\dot{I_b}=\dot{I_c}\)より
\[\dot{I_0}+a^2\dot{I_1}+a\dot{I_2}=\dot{I_0}+a\dot{I_1}+a^2\dot{I_2}\]
両辺を\(\dot{I_0}\)で引くことで、
\[a^2\dot{I_1}+a\dot{I_2}=a\dot{I_1}+a^2\dot{I_2}\]
\(\dot{I_1}\)、\(\dot{I_2}\)を移項して
\[\dot{I_1}(a^2-a)=\dot{I_2}(a^2-a)\]
両辺を\(a^2-a\)で割ることで
\[\dot{I_1}=\dot{I_2}\]
\(\dot{I_b}=0\)(または\(\dot{I_c}=0\)より)
\[\dot{I_b}=\dot{I_0}+a^2\dot{I_1}+a\dot{I_2}=\dot{I_0}+\dot{I_1}(a^2+a)=0\]
ベクトルオペレータの性質 \(1+a^2+a=0 \to a^2+a=-1\)より
\[\dot{I_b}=\dot{I_0}-\dot{I_1}=0\]
移項して
\[\dot{I_0}=\dot{I_1}\]
上式より
\[\dot{I_0}=\dot{I_1}=\dot{I_2}\]
零相電流、正相電流、逆相電流が等しいことがわかりました!
ここで、\(\dot{I_a}=\dot{I_0}+\dot{I_1}+\dot{I_2}\)より
\[\dot{I_a}=3\dot{I_0}\]
地絡電流は零相電流の3倍であることがわかります。
電圧に関する式
\(\dot{V_a}\)を変換します。
\[\dot{V_a}=\dot{V_0}+\dot{V_1}+\dot{V_2}\]
発電機の基本式より、
\[\dot{V_0}=-\dot{I_0}\dot{Z_0}\]
\[\dot{V_1}=\dot{E_a}-\dot{I_1}\dot{Z_1}\]
\[\dot{V_2}=-\dot{I_2}\dot{Z_2}\]
これを代入すると、
\[\dot{V_a}=-\dot{I_0}\dot{Z_0}+\dot{E_a}-\dot{I_1}\dot{Z_1}-\dot{I_2}\dot{Z_2}\]
\[\dot{I_0}=\dot{I_1}=\dot{I_2}\]より、
\[\dot{V_a}=-\dot{I_0}\dot{Z_0}+\dot{E_a}-\dot{I_0}\dot{Z_0}-\dot{I_0}\dot{Z_0}\]
零相電流についての導出
\(\dot{I_0}\)について整理すると
\[\dot{V_a}=\dot{E_a}-\dot{I_0}(\dot{Z_0}+\dot{Z_1}+\dot{Z_2})\]
\(\dot{V_a}\)の右辺は\(\dot{I_a}R=3\dot{I_0}R\)より、
\[\dot{E_a}-\dot{I_0}(\dot{Z_0}+\dot{Z_1}+\dot{Z_2})=3\dot{I_0}R\]
\(\dot{I_0}\)について整理して
\[\dot{E_a}=\dot{I_0}(\dot{Z_0}+\dot{Z_1}+\dot{Z_2}+3R)\]
\(\dot{I_0}\)について解くと
\[\dot{I_0}=\frac{\dot{E_a}}{\dot{Z_0}+\dot{Z_1}+\dot{Z_2}+3R}\]
これで完成です。
\(\dot{V_b}\)、\(\dot{V_c}\)についての導出
重要度は低いですが、一応\(V_b\)の導出過程をのせておきましょう。\(\dot{V_c}\)も全く同じ手順です。
\[\dot{V_b}=\dot{V_0}+a^2\dot{V_1}+a\dot{V_2}\]
発電機の基本式を用いて変形すると
\[\dot{V_b}=-\dot{I_0}\dot{Z_0}+a^2\dot{E_a}-a^2\dot{I_0}\dot{Z_1}-a\dot{I_0}\dot{Z_2}\]
\(\dot{I_0}\)について整理して
\[\dot{V_b}=a^2\dot{E_a}-\dot{I_0}(\dot{Z_0}+a^2\dot{Z_1}+a\dot{Z_2})\]
\(\dot{I_0}=\frac{\dot{E_a}}{\dot{Z_0}+\dot{Z_1}+\dot{Z_2}+3R}\)を代入し、
\[\dot{V_b}=a^2\dot{E_a}-\frac{\dot{Z_0}+a^2\dot{Z_1}+a\dot{Z_2}}{\dot{Z_0}+\dot{Z_1}+\dot{Z_2}+3R}\dot{E_a}\]
1つにまとめると、
\[\dot{V_b}=\frac{\dot{Z_0}(a^2-1)+\dot{Z_2}(a^2-a)+3a^2R}{\dot{Z_0}+\dot{Z_1}+\dot{Z_2}+3R}\dot{E_a}\]
同様に、\(\dot{V_c}\)は
\[\dot{V_c}=\frac{\dot{Z_0}(a-1)+\dot{Z_2}(a-a^2)+3a^2R}{\dot{Z_0}+\dot{Z_1}+\dot{Z_2}+3R}\dot{E_a}\]
以上で導出は完了です!
対称分等価回路
\(\dot{I_0}=\dot{I_1}=\dot{I_2}\)より、対称分等価回路は以下のようになります。
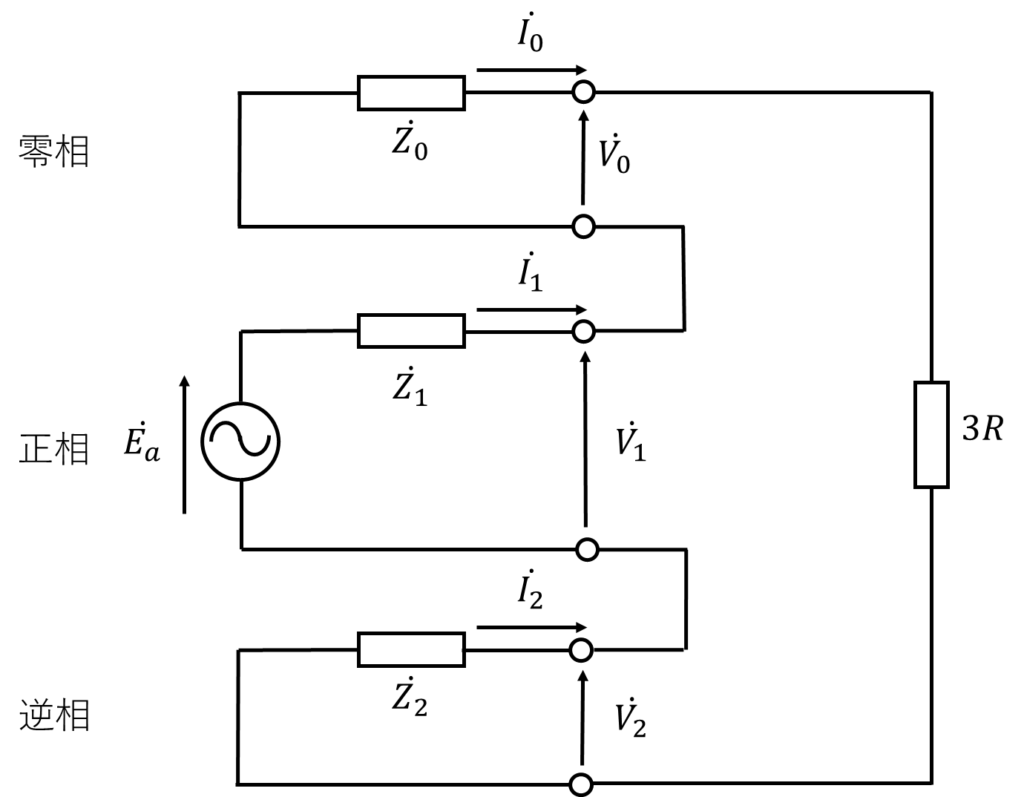
零相、正相、逆相回路が直列に接続されていますね。
正相電圧、対称分インピーダンスで表した式
導出した式をまとめてみます。
\[\dot{I_a}=3\dot{I_0}=\frac{3\dot{E_a}}{\dot{Z_0}+\dot{Z_1}+\dot{Z_2}+3R}\]
\[\dot{V_a}=\dot{I_a}R=\frac{3R}{\dot{Z_0}+\dot{Z_1}+\dot{Z_2}+3R}\dot{E_a}\]
\[\dot{V_b}=\frac{\dot{Z_0}(a^2-1)+\dot{Z_2}(a^2-a)+3a^2R}{\dot{Z_0}+\dot{Z_1}+\dot{Z_2}+3R}\dot{E_a}\]
\[\dot{V_c}=\frac{\dot{Z_0}(a-1)+\dot{Z_2}(a-a^2)+3a^2R}{\dot{Z_0}+\dot{Z_1}+\dot{Z_2}+3R}\dot{E_a}\]
けっこう複雑な式ですね。
これを試験時間内に導出するのはかなり厳しいので、ある程度は暗記しておく必要があります。
一線地絡電流は零相電流の3倍くらいは覚えておきましょう。
まとめ
今回は一線地絡事故を対称座標法を用いた式の導出過程を表してみました!
参考書でも複雑な式が永遠と続いているのでとっつきにくさMAXですが、1つ1つみていくと意外と難しくありません。
電験でもよく出るポイントは決まっているので、パターンがわかればもう得点源です。
二種では一線地絡、一種では二相短絡をよく学習するようにしてください。
以上です☻
おわり



コメント