~円形同軸ケーブルの磁束密度~
問題
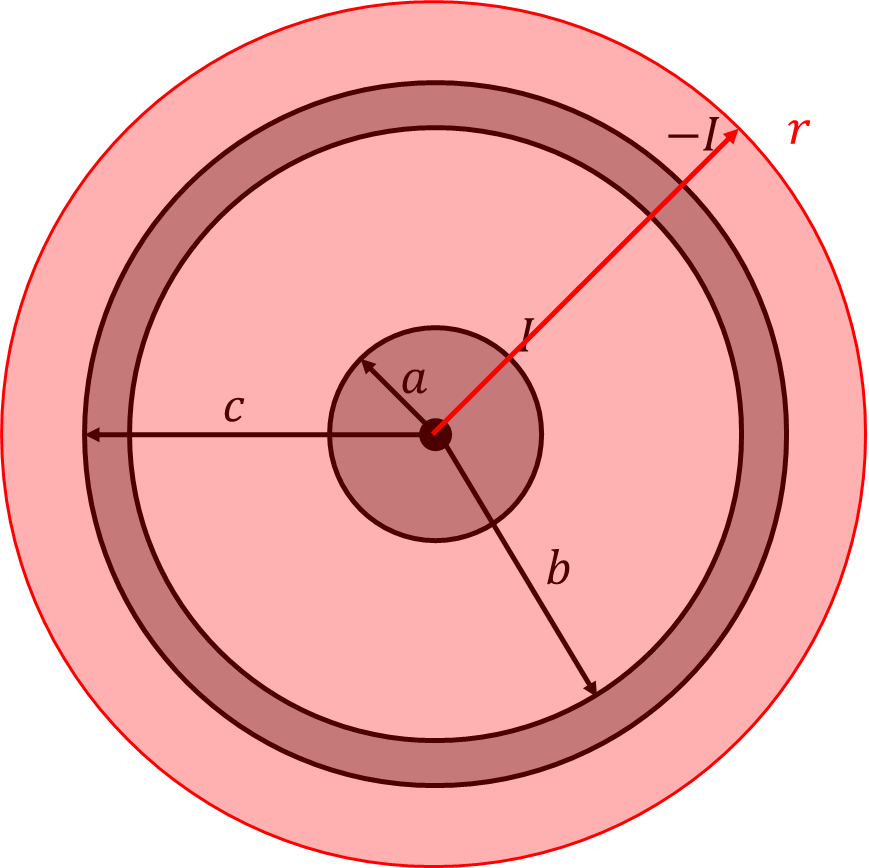
図示のような円形同軸ケーブルの内外導体に、往復電流\(I\)が一様な密度で流れている。各部の磁束密度を半径\(r\)の関数として求め、その分布の概略図を描け。
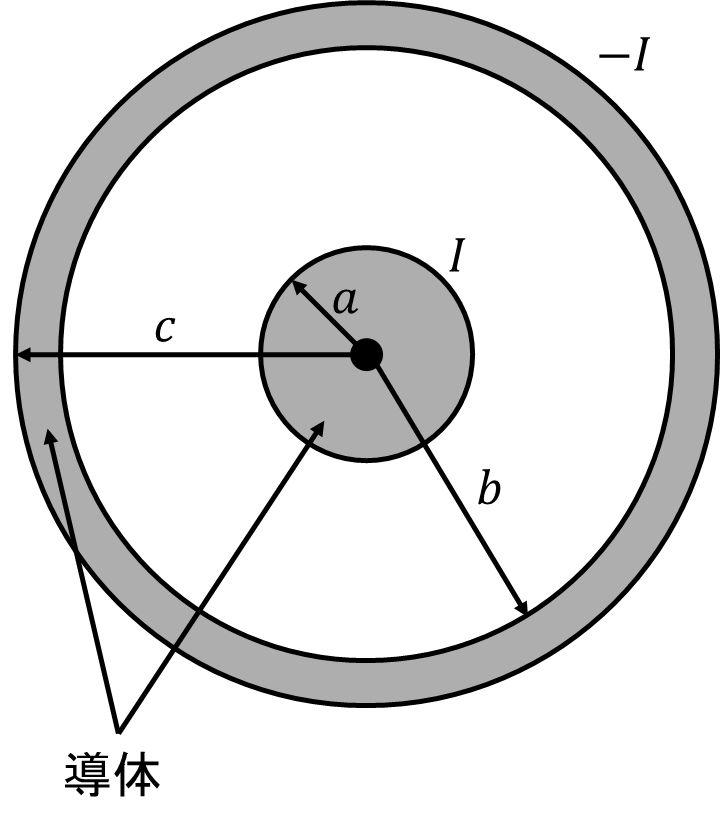
解説
導体が十分に長いとして、そこから\(r\)離れた地点の磁束密度は真空中の透磁率を\(\mu_0\)としてアンペアの周回積分の法則から次式で表せる。
\[\oint_c B\cdot dl=\mu_0 I\]
\[2\pi rB=\mu_0 I\to B=\frac{\mu_0 I}{2\pi r}\]
\(0 <r \leqq a\)のとき
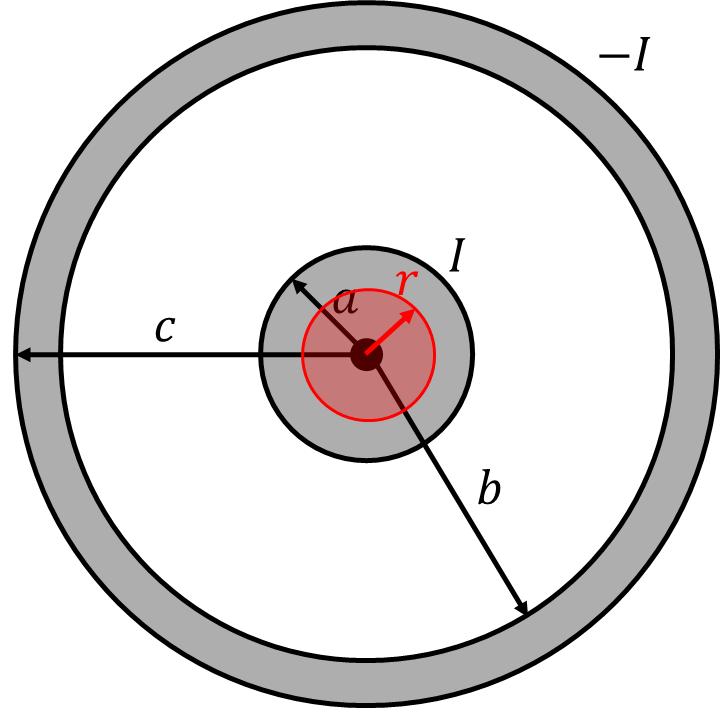
閉曲線内を通過する電流\(I(r)\)は、導体には一様に電流が流れていることから電流密度で求める。
\[I(r)=\frac{I}{\pi a^2}\times \pi r^2=\frac{r^2}{a^2}I\]
\(B(r)=\frac{\mu_0 I(r)}{2\pi r}\)より
\[B(r)=\frac{\mu_0}{2\pi r}\times \frac{r^2}{a^2}I=\frac{\mu_0 rI}{2\pi a^2}\]
よって、\(r\)に比例する。
\(a<r\leqq b\)のとき
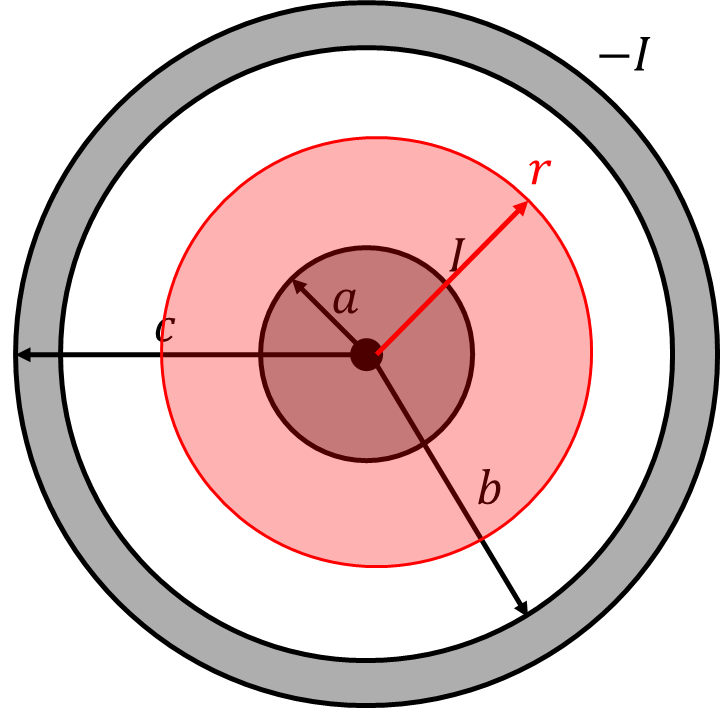
上記と同様に電流を求めると、\(I\)となる。よって、
\[B(r)=\frac{\mu_0 I}{2\pi r}\]
より、\(r\)に反比例する。
\(b<r\leqq c\)のとき
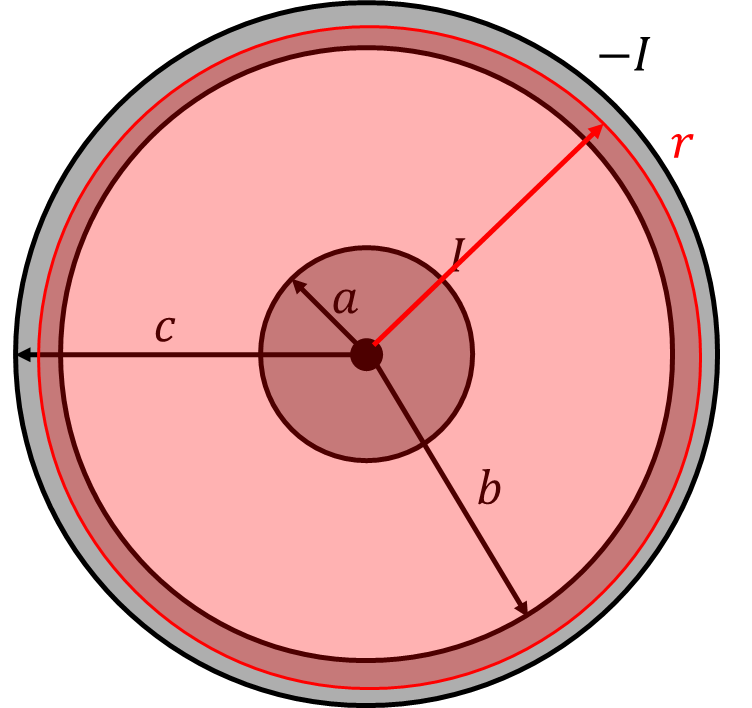
上記と同様に電流を求めると、
\[I(r)=I+\frac{\pi(r^2-b^2)}{\pi(c^2-b^2)}(-I)=\frac{c^2-r^2}{c^2-b^2}I\]
代入し、
\[B(r)=\frac{\mu_0}{2\pi r}\times \frac{c^2-r^2}{c^2-b^2}I=\frac{\mu_0 I(c^2-r^2)}{2\pi r(c^2-b^2)}\]
\(c<r\)のとき
閉曲線内の電流は
\[I(r)=I+(-I)=0\]
より、\(B(r)=0\)となる。
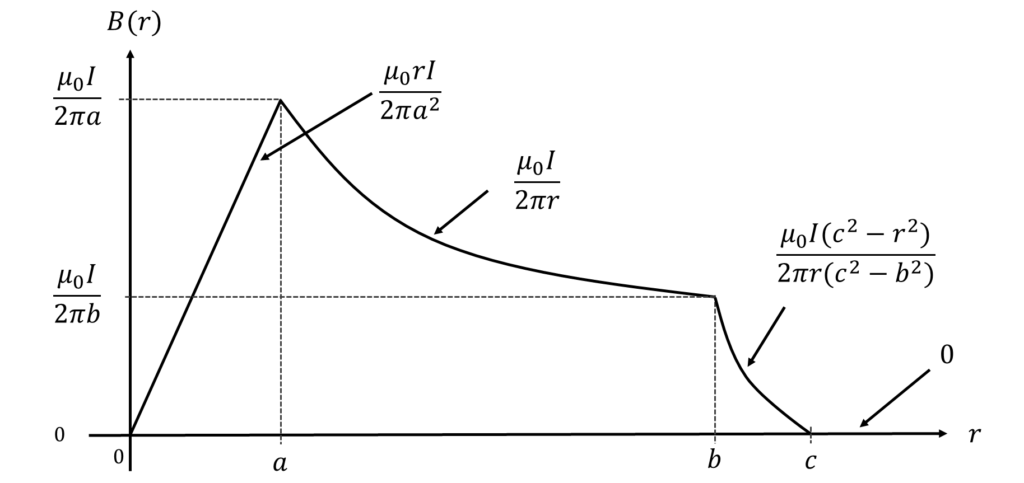
グラフ化
\(0 <r \leqq a\)のとき\(B(r)=\frac{\mu_0 rI}{2\pi a^2}\)
\(a<r\leqq b\)のとき\(B(r)=\frac{\mu_0 I}{2\pi r}\)
\(b<r\leqq c\)のとき\(B(r)=\frac{\mu_0 I(c^2-r^2)}{2\pi r(c^2-b^2)}\)
\(c<r\)のとき\(B(r)=0\)
これらをまとめると、以下のグラフとなる。
出典
昭和60年度第二種電気主任技術者筆記試験理論問1




コメント