今回はみんな大好き分布定数回路についてみていきます!
分布定数回路とは?
電気回路には、プリント基板のような短距離のものから送電線路のような長距離のものまでさまざま。短距離と長距離では、同じ等価回路を描いて解析すると誤差が大きくなり、使い物になりません。
そこで、等価回路をもう少し複雑にすることで誤差を少なくします。
主に、電気信号の波長に比べて線路が十分に長いときに分布定数回路、そうでないときは集中定数回路を使います。
回路図
分布定数回路では、回路素子が線路に沿って一様に分布していると考えます。
三相回路では、一相あたりで考えます。
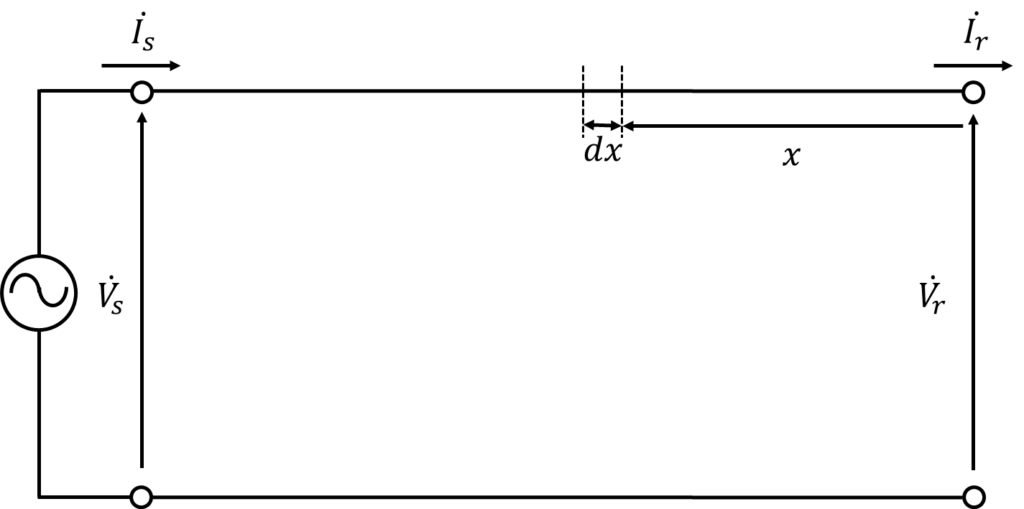
受電端から\(x\)の地点での微小距離\(dx\)の要素が以下の図のようになっているとします。
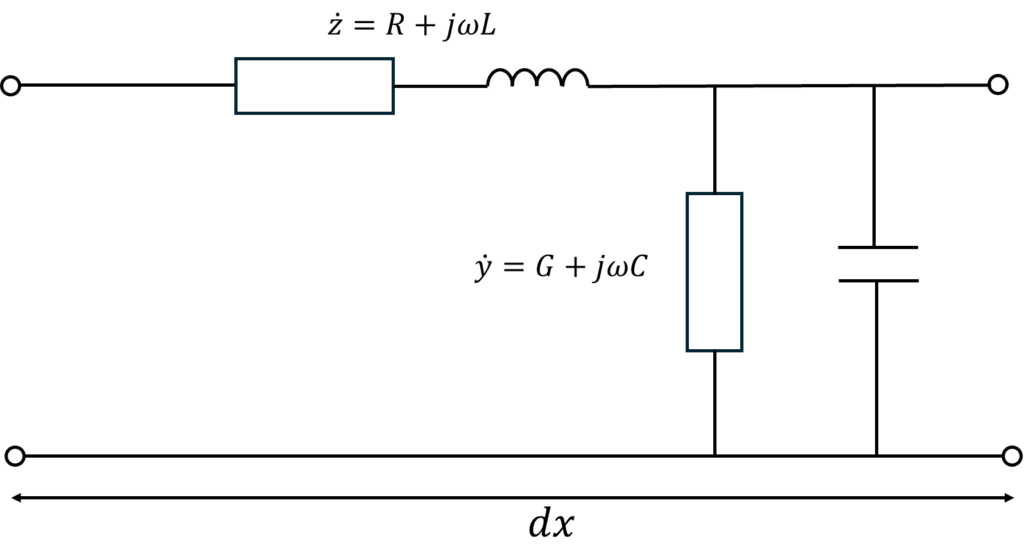
ここで、回路定数を以下のように定めています。
\(R\):単位長あたりの線路抵抗[Ω/m]
\(L\):単位長あたりの線路インダクタンス[H/m]
\(G\):単位長あたりの線路間の漏れコンダクタンス[S/m]
\(C\):単位長あたりの線路間の静電容量[F/m]
線路方程式の導出
\(x\)での電圧を\(\dot{V}\)、電流を\(\dot{I}\)とします。
微小距離\(dx\)での電圧降下を\(d\dot{V}\)、電流変化を\(d\dot{I}\)とすると、
\[d\dot{V}=\dot{I}\dot{z}dx\to \frac{\dot{dV}}{dx}=\dot{I}\dot{z}\]
\[d\dot{I}=\dot{V}\dot{y}dx\to \frac{\dot{dI}}{dx}=\dot{V}\dot{y}\]
\(\frac{d}{dx}(\frac{d\dot{V}}{dx})=\dot{z}\frac{d\dot{I}}{dx}\)より、
\[\frac{d^2\dot{V}}{dx^2}=\dot{z}\dot{y}\dot{V}\]
定数\(k\)、\(\dot{\lambda}\)を用いて\(\dot{V}=Ke^{\dot{\lambda}x}\)とおき、2階微分方程式を解くと
\[\dot{\lambda} ^2ke^{\dot{\lambda}x}=\dot{x}\dot{y}ke^{\dot{\lambda}x}\to \dot{\lambda}=\pm\sqrt{\dot{x}\dot{y}}\]
\[\dot{V}=k_1e^{\dot{\lambda}x}+k_2e^{-\dot{\lambda}x}\]
\(\dot{I}=\frac{1}{\dot{z}}\frac{d\dot{V}}{dx}\)より、
\[\dot{I}=\frac{1}{\dot{z}}(k_1\dot{\lambda}e^{\dot{\lambda}x}-k_2\dot{\lambda}e^{-\dot{\lambda}x})\]
ここで、\(\dot{\lambda}=\sqrt{\dot{x}\dot{y}}\)は伝搬定数といわれます。
次に、定数\(k_1\)、\(k_2\)を求めます。\(x\)=0で\(\dot{V}=\dot{V_r}\)、\(\dot{I}=\dot{I_r}\)となるため、
\[\dot{V_r}=k_1+k_2\]
\[\dot{I_r}=\frac{1}{\dot{z}}(k_1\dot{\lambda}-k_2\dot{\lambda})\]
よって、
\[k_1=\frac{1}{2}(\dot{V_r}+\frac{\dot{z}}{\dot{\lambda}}\dot{I_r})\]\[k_2=\frac{1}{2}(\dot{V_r}-\frac{\dot{z}}{\dot{\lambda}}\dot{I_r})\]
線路長を\(l\)としたとき、\(x=l\)で\(\dot{V}=\dot{V_s}\)、\(\dot{I}=\dot{I_s}\)となるため、
\[\dot{V_s}=k_1e^{\dot{\lambda}l}+k_2e^{-\dot{\lambda}l}=\frac{1}{2}(\dot{V_r}+\frac{\dot{z}}{\dot{\lambda}}\dot{I_r})e^{\dot{\lambda}l}+\frac{1}{2}(\dot{V_r}-\frac{\dot{z}}{\dot{\lambda}}\dot{I_r})e^{\dot{\lambda}l}\]
\[=\dot{V_r}\frac{e^{\dot{\lambda}l}+e^{-\dot{\lambda}l}}{2}+\sqrt{\frac{\dot{z}}{\dot{y}}}\dot{I_r}\frac{e^{\dot{\lambda}l}-e^{-\dot{\lambda}l}}{2}\]
\[=\dot{V_r}\cosh{(\dot{\lambda}l)}+\dot{Z_w}\dot{I_r}\sinh{(\dot{\lambda}l)}\]
\[\dot{I_s}=\frac{1}{\dot{z}}(k_1\dot{\lambda}e^{\dot{\lambda}l}-k_2\dot{\lambda}e^{-\dot{\lambda}l})=\frac{\dot{\lambda}}{2\dot{z}}(\dot{V_r}+\frac{\dot{z}}{\dot{\lambda}}\dot{I_r})e^{\dot{\lambda}l}-\frac{\dot{\lambda}}{2\dot{z}}(\dot{V_r}-\frac{\dot{z}}{\dot{\lambda}}\dot{I_r})e^{-\dot{\lambda}l}\]
\[=\sqrt{\frac{\dot{y}}{\dot{z}}}\dot{V_r}\frac{e^{\dot{\lambda}l}-e^{-\dot{\lambda}l}}{2}+\dot{I_r}\frac{e^{\dot{\lambda}l}+e^{\dot{-\lambda}l}}{2}\]
\[=\frac{\dot{V_r}}{\dot{Z_w}}\sinh{(\dot{\lambda}l)}+\dot{I_r}\cosh{(\dot{\lambda}l)}\]
ここで、\(\dot{Z_w}=\sqrt{\frac{\dot{z}}{\dot{y}}}\)は特性インピーダンスといわれます。
無損失線路では\(R=G=0\)であることから、
\[\dot{Z_w}=\sqrt{\frac{\dot{z}}{\dot{y}}}=\sqrt{\frac{R+j\omega L}{G+j\omega C}}=\sqrt{\frac{L}{C}}\]
となります。
まとめ
線路が波長に比べて十分に長いとき、複雑な回路で解析する必要があります。
でも、プリント基板上のごく短い回路でも、高周波を扱うとなれば特に静電容量の影響が無視できなくなります。
CPUなんかでは回路を小さくして多くの素子を埋め込んで高性能化したい半面、静電容量の充電電流で動作が遅くなってしまいます。
送電線路でも、対地静電容量を介して微小な電流が流れています。
これらの影響を考慮するのが分布定数回路なのです。
四端子定数とともに理解しておきましょう。
では!
おわり



コメント