~直流電源・交流電源の複合回路~
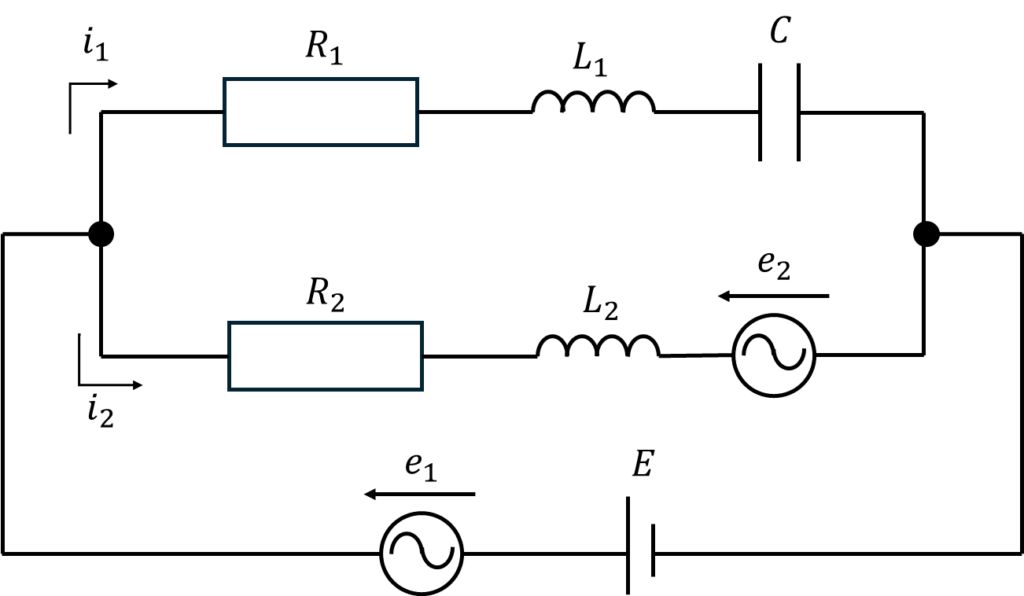
問題
図示のような回路において、抵抗\(R_1\)及び\(R_2\)を流れる電流の瞬時値\(i_1\)及び\(i_2\)を求めよ。ただし、\(E\)は直流起電力で、\(e_1\)及び\(e_2\)はそれぞれ次式で表される交流起電力とし、また、\(L_1\)及び\(L_2\)はインダクタンス、\(C\)は静電容量とする。
\[e_1=\sqrt2 E_1 \sin{(\omega t+\phi_1)}\]
\[e_2=\sqrt2 E_2 \sin{(2\omega t+\phi_2)}\]
解答
\[i_1=\frac{\sqrt2 E_1}{\sqrt{R_1^2+(\omega L_1-\frac{1}{\omega C})^2}}\sin{(\omega t+\phi_1-\theta_{11})}\]
\[i_2=\frac{E}{R_2}+\frac{\sqrt2 E_1}{\sqrt{R_1^2+(\omega L_1)^2}}\sin{(\omega t+\phi_1-\theta_{21})}-\frac{\sqrt2 E_2}{\sqrt{R_2^2+(2\omega L_2)^2}}\sin{(2\omega L_2+\phi_2-\theta_2)}\]
解説
重ね合わせの理による解法
交流電圧源を短絡除去したときの回路
交流電圧源を短絡除去したときの回路は図のようになる。
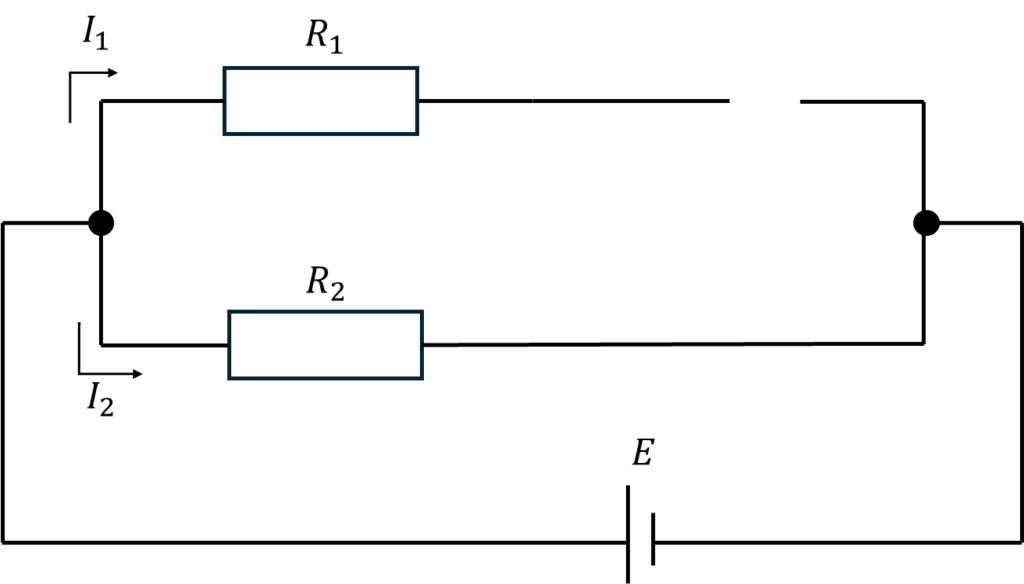
直流(周波数ゼロ)に対しては、インダクタは短絡、コンデンサは開放となる。
\[I_1=0、I_2=\frac{E}{R_2}\]
直流電圧源、交流電圧源\(e_2\)を短絡除去したときの回路
直流電圧源、交流電圧源\(e_2\)を短絡除去したときの回路は図のようになる。
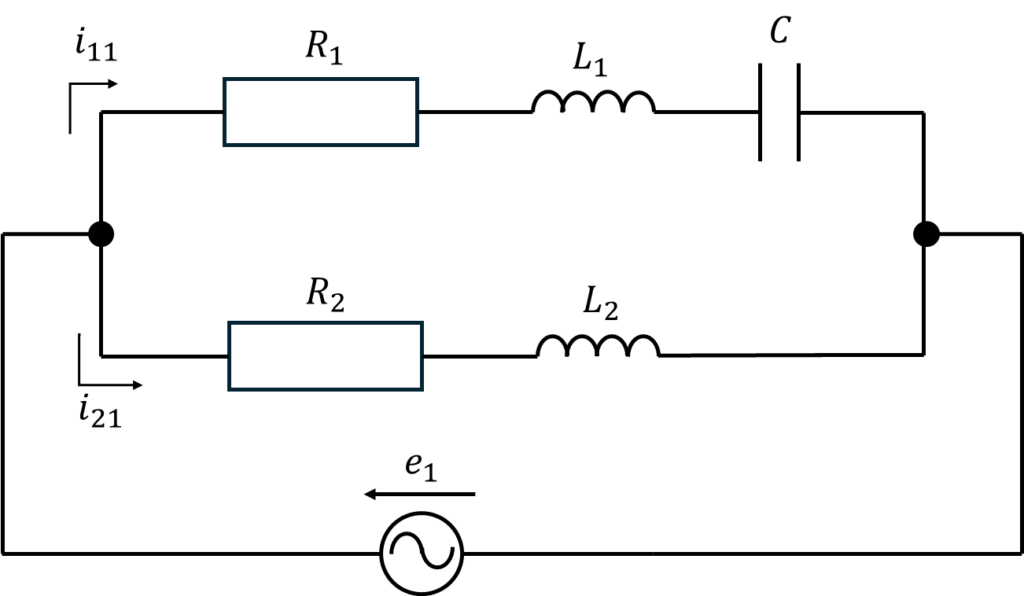
\[i_{11}=\frac{\sqrt2 E_1}{\sqrt{R_1^2+(\omega L_1-\frac{1}{\omega C})^2}}\sin{(\omega t+\phi_1-\theta_{11})}\]
\[i_{21}=\frac{\sqrt2 E_1}{\sqrt{R_1^2+(\omega L_1)^2}}\sin{(\omega t+\phi_1-\theta_{21})}\]
ただし、
\[\theta_{11}=\tan^{-1}{\frac{\omega L_1 -\frac{1}{\omega C}}{R_1}}、\theta_{21}=\tan^{-1}{\frac{\omega L_2}{R_2}}\]
\(i_{11}\)は、リアクタンス\(\omega L_1-\frac{1}{\omega C}\)の分だけ位相が遅れ、
\(i_{21}\)は、リアクタンス\(\omega L_2\)の分だけ位相が遅れる。
直流電圧源、交流電圧源\(e_1\)を短絡除去したときの回路
直流電圧源、交流電圧源\(e_1\)を短絡除去したときの回路は図のようになる。

\(e_1\)、\(E\)のあったブランチは短絡されていることから、\(i_{12}\)には電流が流れない。
\[i_{12}=0\]
\[i_{22}=-\frac{\sqrt2 E_2}{\sqrt{R_2^2+(2\omega L_2)^2}}\sin{(2\omega L_2+\phi_2-\theta_2)}\]
ただし、
\[\theta_2=\tan^{-1}{\frac{2\omega L_2}{R_2}}\]
重ね合わせ
\(i_1=I_1+i_{11}+i_{21}\)
\(=0+\frac{\sqrt2 E_1}{\sqrt{R_1^2+(\omega L_1-\frac{1}{\omega C})^2}}\sin{(\omega t+\phi_1-\theta_{11})}+0\)
\(=\frac{\sqrt2 E_1}{\sqrt{R_1^2+(\omega L_1-\frac{1}{\omega C})^2}}\sin{(\omega t+\phi_1-\theta_{11})}\)
\(i_2=I_2+i_{12}+i_{22}\)
\(=\frac{E}{R_2}+\frac{\sqrt2 E_1}{\sqrt{R_1^2+(\omega L_1)^2}}\sin{(\omega t+\phi_1-\theta_{21})}-\frac{\sqrt2 E_2}{\sqrt{R_2^2+(2\omega L_2)^2}}\sin{(2\omega L_2+\phi_2-\theta_2)}\)
複素電源への変換による解法
与えられた電圧源を複素電圧源へ変換する。
\[\dot{E}=E\]
\[\dot{E_1}=E_1 e^{j(\omega t+\phi_1)}\]
\[\dot{E_2}=E_2 e^{j(2\omega t+\phi_2)}\]
この複素電圧源の虚数をとることでもとの瞬時電圧に変換できる。
また、求める電流\(i_1\)、\(i_2\)を複素電流\(\dot{I_1}\)、\(\dot{I_2}\)とする。
\(\dot{I_1}\)について
コンデンサ\(C\)が含まれるため、\(\dot{I_1}\)は\(\dot{E}\)に依存しない。
\[\dot{I_1}=\frac{\dot{E_1}}{R_1+j(\omega L_1-\frac{1}{\omega C})}\]
\[=\frac{E_1}{\sqrt{R_1^2+(\omega L_1-\frac{1}{\omega C})^2}}e^{j(\omega t+\phi_1-\theta_1)}\]
ただし、
\[\theta_1=\tan^{-1}{\frac{\omega L_1}{R_1}}\]
\(\dot{I_2}\)について
それぞれの複素電圧源に作用する複素インピーダンスの値が異なることから、それぞれについて検討する。
\(\dot{E}\)による電流\(\dot{I_{20}}\)
直流電圧源に対しては、インダクタは短絡となることから、
\[\dot{I_{20}}=\frac{E}{R_2}\]
\(\dot{E_1}\)による電流\(\dot{I_{21}}\)
重ね合わせの理と同じように、
\[\dot{I_{21}}=\frac{E_1}{\sqrt{R_2^2+(\omega L_2)^2}}e^{j(\omega L_2+\phi_1-\theta_{21})}\]
ただし、
\[\theta_{21}=\tan^{-1}{\frac{\omega L_2}{R_2}}\]
\(\dot{E_2}\)による電流\(\dot{I_{22}}\)
重ね合わせの理と同じように、
\[\dot{I_{22}}=-\frac{E_2}{\sqrt{R_2^2+(2\omega L_2)^2}}e^{j(\omega L_2+\phi_1-\theta_{22})}\]
ただし、
\[\theta_{22}=\tan^{-1}{\frac{2\omega L_2}{R_2}}\]
瞬時値へ逆変換
\[\dot{I_1}=\frac{E_1}{\sqrt{R_1^2+(\omega L_1-\frac{1}{\omega C})^2}}e^{j(\omega t+\phi_1-\theta_1)}\]
\[\dot{I_{2}}=\frac{E}{R_2}+\frac{E_1}{\sqrt{R_2^2+(\omega L_2)^2}}e^{j(\omega L_2+\phi_1-\theta_{21})}-\frac{E_2}{\sqrt{R_2^2+(2\omega L_2)^2}}e^{j(\omega L_2+\phi_1-\theta_{22})}\]
\(\sqrt2\)倍し、虚数をとると
\[\dot{I_1}=\frac{\sqrt2 E_1}{\sqrt{R_1^2+(\omega L_1-\frac{1}{\omega C})^2}}\sin{(\omega t+\phi_1-\theta_{1})}\]
\[\dot{I_2}=\frac{E}{R_2}+\frac{\sqrt2 E_1}{\sqrt{R_1^2+(\omega L_1)^2}}\sin{(\omega t+\phi_1-\theta_{21})}-\frac{\sqrt2 E_2}{\sqrt{R_2^2+(2\omega L_2)^2}}\sin{(2\omega L_2+\phi_2-\theta_{22})}\]
ただし、
\[\theta_{1}=\tan^{-1}{\frac{\omega L_1}{R_1}}、\theta_{21}=\tan^{-1}{\frac{\omega L_2}{R_2}}、\theta_{22}=\tan^{-1}{\frac{2\omega L_2}{R_2}}\]
出典
昭和60年度第二種電気主任技術者筆記試験理論問2



コメント