~単相電力計を用いた三相電力の計算~
問題
2個の単相電力計A及びBを図のように三相3線式平衡回路に接続した場合について、次の問に答えよ。ただし、星形電圧\(\dot{V_a}\)と線電流\(\dot{I_a}\)との位相差を\(\phi\)(遅れ電流)とし、相順を\(a\to b\to c\)とする。
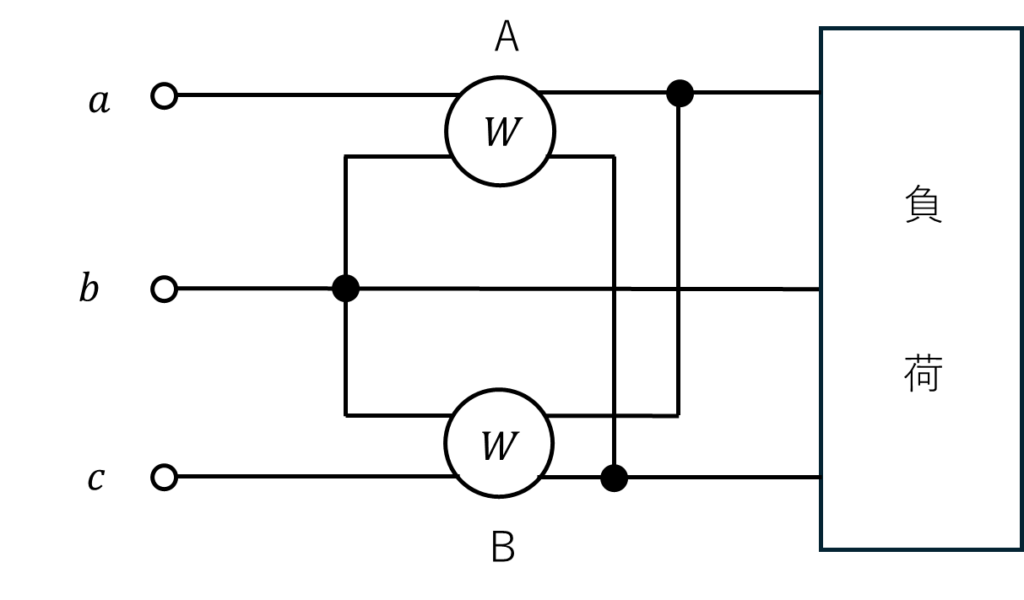
(1)電力計Aの指示は、どのような値となるか。また、この値は、この三相平衡回路の無効電力とどのような関係にあるか。
(2)電力計A及びBの指示の和は、どんな値となるか。
解答
(1)電力計Aの指示は
\[\sqrt{3}|\dot{V_a}||\dot{I_a}|\sin{\phi}\]
よって、回路無効電力の\(\frac{1}{\sqrt{3}}\)と等しい。
(2)電力計AとBの指示の和は\(0\)となる。
解説
(1)
この回路のフェーザ図を示す。
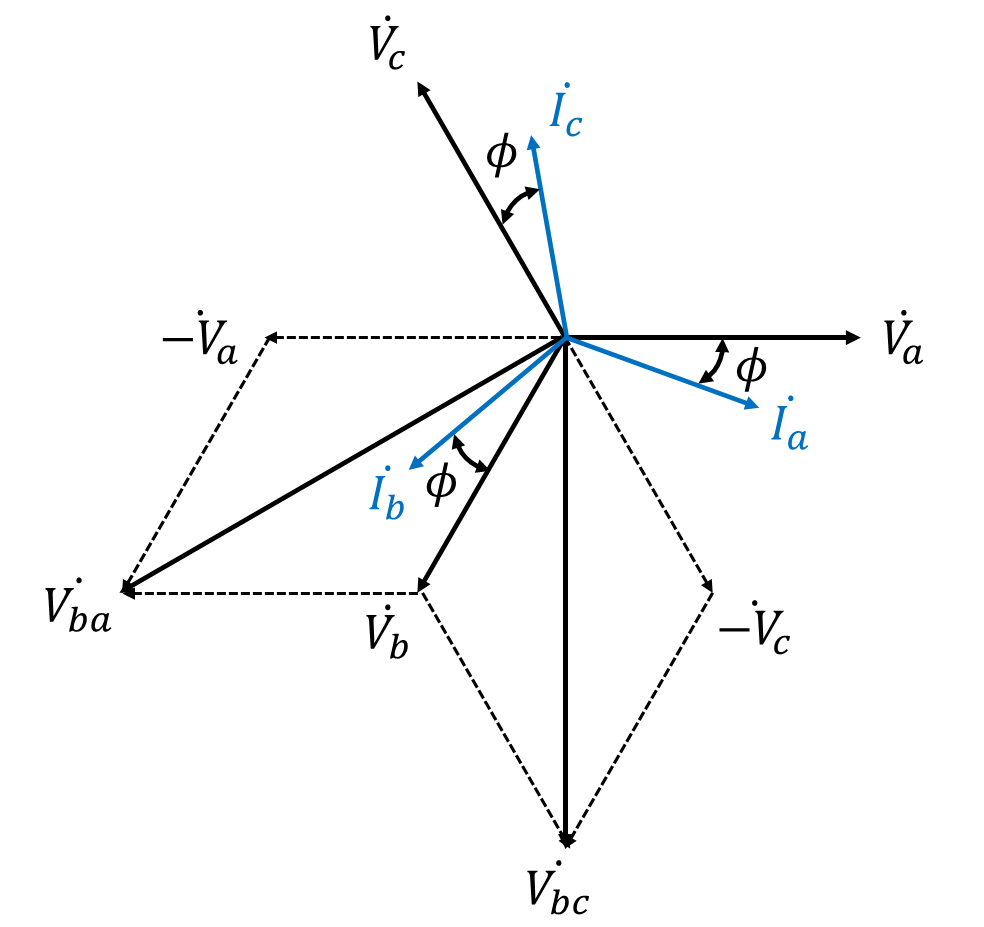
電力計Aの指示値\(P_A\)は、電圧コイルにかかる電圧\(\dot{V_{bc}}\)の大きさと電流コイルに流れる電流\(\dot{I_a}\)の大きさに、両者の位相差の余弦を乗じたものとなる。
\[P_A=|\dot{V_{bc}}||\dot{I_a}|\cos{(\frac{\pi}{2}-\phi)}\]
線間電圧の大きさは星形電圧の\(\sqrt{3}\)倍、三角関数の加法定理\(\cos{(\alpha-\beta)}=\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}\)を用いて、
\[P_A=|\dot{V_{bc}}||\dot{I_a}|\cos{(\frac{\pi}{2}-\phi)}=\sqrt{3}|\dot{V_a}||\dot{I_a}|\sin{\phi}\]
ここで、回路で消費される無効電力は
\[3|\dot{V_a}||\dot{I_a}|\sin{\phi}\]
であるから、電力計Aの指示値を\(\sqrt{3}\)倍することで回路全体の消費無効電力となる。
\(\dot{V_a}\)が相電圧であることに留意する。
(2)
次に、電力計Bの指示値\(P_B\)を求める。
\[P_B=|\dot{V_{ba}}||\dot{I_c}|\cos{(\frac{\pi}{2}+\phi)}=-\sqrt{3}|\dot{V_a}||\dot{I_a}|\sin{\phi}\]
よって、
\[P_A=\sqrt{3}|\dot{V_a}||\dot{I_a}|\sin{\phi}\]
\[P_B=-\sqrt{3}|\dot{V_a}||\dot{I_a}|\sin{\phi}\]
となり、両者の和は\(0\)である。
ちなみに、電圧コイルの極性を考慮する必要があり、特に電力計Bの電圧コイルにかかる電圧は\(\dot{V_{ba}}\)であることに留意する。
出典
昭和57年度第二種電気主任技術者筆記試験理論問3



コメント