~同心導体球における電界~
問題
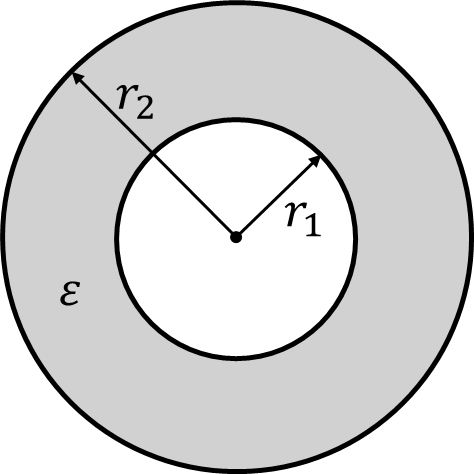
図のように内球の半径\(r_1\)、外球の内半径\(r_2\)の二つの同心導体球があり、その間に誘電率\(\varepsilon\)の絶縁体が満たされている。外球の内半径\(r_2\)及び両球間の電位差\(V\)をそれぞれ一定とした場合、内球の表面における電界の強さを最小にするには、その半径\(r_1\)をいくらにすればよいか。
解答
内球表面の電界を最小にする半径\(r_1\)は
\[r_1=\frac{r_2}{2}\]
解説
\(Q\)[C]の電荷をもつ導体球の中心から\(r\)の地点の電界は、誘電率を\(\varepsilon\)とすると、ガウスの法則より次式で求められる。
\[\oint{E\cdot ds}=\frac{Q}{\varepsilon}\]
\[4\pi r^2E=\frac{Q}{\varepsilon}\to E=\frac{Q}{4\pi \varepsilon r^2}\]
ただし、導体球内の電界は\(0\)である。
\(r_1\)、\(r_2\)間の電位\(V\)は、定義より
\[V=-\int_{r_2}^{r_1}{E\cdot dr}=\frac{Q}{4\pi \varepsilon}\int_{r_2}^{r_1}{\frac{1}{r^2}}=\frac{Q}{4\pi r^2}\left(\frac{1}{r_1}-\frac{1}{r_2}\right)\]
\(V\)、\(r_2\)が一定であることから、\(Q\)は\(r_1\)の関数となる。
\[Q=\frac{4\pi \varepsilon V}{\frac{1}{r_1}-\frac{1}{r_2}}\]
これを導体球表面の電界の式に代入し、
\[E=\frac{Q}{4\pi \varepsilon r_1^2}=\frac{\frac{4\pi \varepsilon V}{\frac{1}{r_1}-\frac{1}{r_2}}}{4\pi \varepsilon r_1^2}=\frac{V}{r_1-\frac{r_1^2}{r_2}}=\frac{Vr_2}{r_1r_2-r_1^2}\]
導体球表面の電界が最小になるとき、\(r_1\)は\(E\)の分母が最大値をとるときの値となる。
\(E\)の分母を抜き出し、これを\(y\)とおくと、\(\frac{dy}{dr_1}=0\)となるときの\(r_1\)が\(y\)の最大値となる。
\[\frac{dy}{dr_1}=\frac{d}{dr_1}\left(r_1r_2-r_1^2\right)=r_2-2r_1=0\]
よって、
\[r_1=\frac{r_2}{2}\]
出典
昭和57年度第二種電気主任技術者筆記試験理論問1



コメント