電線3本のうち2本がつながっちゃった!って事故です。
どう解析していくのでしょうか?
どうして二相短絡が起こるの?
自然災害の多い国、日本。送電線に強風が吹くことで2線が短絡します。
また、スリートジャンプやギャロッピングによる電線の跳躍でも接触します。
モデル化した系統より
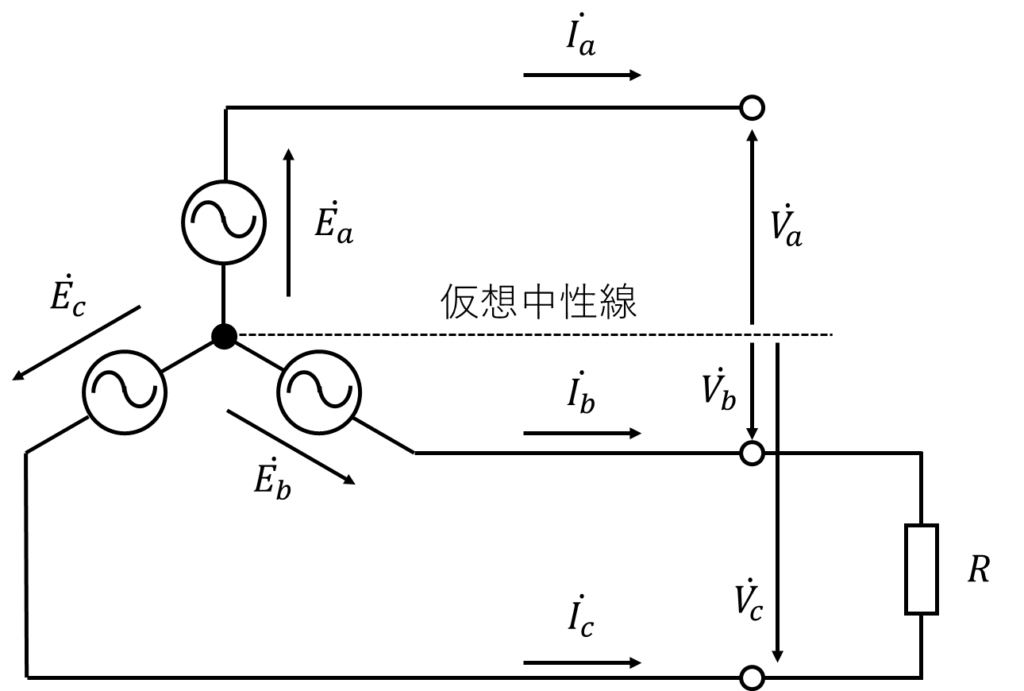
図の系統を用いて解説します。
\(b\)、\(c\)相にて、抵抗\(R\)を介して短絡しています。
短絡電流は\(\dot{I_b}\)(または\(-\dot{I_c}\))です。
これを正相電圧、対称分インピーダンスで表します。
故障条件を求める
故障条件を書き出していきます。
\(a\)相は開放されていることから、
\[\dot{I_a}=0\]
\(b\)、\(c\)相は短絡していることから、
\[\dot{I_b}=-\dot{I_c}\]
オームの法則より、
\[\dot{V_b}=\dot{V_c}+\dot{I_b}R\]
対称分へ変換
電流に関する式
\(\dot{I_b}\)、\(\dot{I_c}\)を対称分へ変換すると、
\[\dot{I_b}=\dot{I_0}+a^2\dot{I_1}+a\dot{I_2}\]
\[\dot{I_c}=\dot{I_0}+a\dot{I_1}+a^2\dot{I_2}\]
\(\dot{I_b}=-\dot{I_c}\)より、
\[\dot{I_0}+a^2\dot{I_1}+a\dot{I_2}=-\dot{I_0}-a\dot{I_1}-a^2\dot{I_2}\]
両辺を\(\dot{I_0}\)で引くことで、
\[a^2\dot{I_1}+a\dot{I_2}=-a\dot{I_1}-a^2\dot{I_2}\]
\(\dot{I_1}\)、\(\dot{I_2}\)を移項して
\[\dot{I_1}(a^2+a)=-\dot{I_2}(a^2+a)\]
両辺を\(a^2+a\)で除すことで
\[\dot{I_1}=-\dot{I_2}\]
\(\dot{I_a}=0\)より、
\[\dot{I_a}=\dot{I_0}+\dot{I_1}+\dot{I_2}=\dot{I_0}+\dot{I_1}-\dot{I_1}=\dot{I_0}=0\]
以上より
\[\dot{I_0}=0\]
\[\dot{I_1}=-\dot{I_2}\]
正相電流\(\dot{I_1}\)の導出
まず\(\dot{I_b}\)を求める。
\[\dot{I_b}=\dot{I_0}+a^2\dot{I_1}+a\dot{I_2}=0+a^2\dot{I_1}-a\dot{I_1}=\dot{I_1}(a^2-a)\]
\(\dot{V_b}=\dot{V_c}+\dot{I_b}R\)より、
\[\dot{V_0}+a^2\dot{V_1}+a\dot{V_2}=\dot{V_0}+a\dot{V_1}+a^2\dot{V_2}+\dot{I_1}R(a^2-a)\]
対称分電圧\(\dot{V_0}\)、\(\dot{V_1}\)、\(\dot{V_2}\)を対称分電流、インピーダンスで表し
\[-\dot{I_0}\dot{Z_0}+a^2\dot{E_a}-a^2\dot{I_1}\dot{Z_1}-a\dot{I_2}\dot{Z_2}=-\dot{I_0}\dot{Z_0}+a\dot{E_a}-a\dot{I_1}\dot{Z_1}-a^2\dot{I_2}\dot{Z_2}+\dot{I_1}R(a^2-a)\]
\[\dot{E_a}(a^2-a)-\dot{I_1}\dot{Z_1}(a^2-a)+\dot{I_2}\dot{Z_2}(a^2-a)=\dot{I_1}R(a^2-a)\]
両辺を\(a^2-a\)で除し
\[\dot{E_a}-\dot{I_1}\dot{Z_1}+\dot{I_2}\dot{Z_2}=\dot{I_1}R\]
\(\dot{I_1}\)について解くと
\[\dot{E_a}=\dot{I_1}(\dot{Z_1}+\dot{Z_2}+R)\to \dot{I_1}=\frac{\dot{E_a}}{\dot{Z_1}+\dot{Z_2}+R}\]
短絡電流\(\dot{I_b}\)、\(\dot{I_b}\)の導出
\(\dot{I_1}=\frac{\dot{E_a}}{\dot{Z_1}+\dot{Z_2}+R}\)より、
\[\dot{I_b}=\dot{I_0}+a^2\dot{I_1}+a\dot{I_2}=\frac{a^2}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}-\frac{a}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}\]
ベクトルオペレータの性質\(a^2-a=-j\sqrt{3}\)より、
\[\dot{I_b}=\frac{a^2-a}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}=-j\frac{\sqrt{3}\dot{E_a}}{\dot{Z_1}+\dot{Z_2}+R}\]
また、\(\dot{I_c}=-\dot{I_b}\)より、
\[\dot{I_c}=j\frac{\sqrt{3}\dot{E_a}}{\dot{Z_1}+\dot{Z_2}+R}\]
\(\dot{V_a}\)、\(\dot{V_b}\)、\(\dot{V_c}\)の導出
\(\dot{V_a}\)を求める。
\[\dot{V_a}=\dot{V_0}+\dot{V_1}+\dot{V_2}=-\dot{I_0}\dot{Z_0}+\dot{E_a}-\dot{I_1}\dot{Z_1}-\dot{I_2}\dot{Z_2}\]
\[=\dot{E_a}-\dot{I_1}\dot{Z_1}+\dot{I_1}\dot{Z_2}=\dot{E_a}-\dot{I_1}(\dot{Z_1}-\dot{Z_2})\]
\[=\dot{E_a}-\frac{\dot{Z_1}-\dot{Z_2}}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}=\frac{2\dot{Z_2}+R}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}\]
\(\dot{V_b}\)を求める。
\[\dot{V_b}=\dot{V_0}+a^2\dot{V_1}+a\dot{V_2}=-\dot{I_0}\dot{Z_0}+a^2\dot{E_a}-a^2\dot{I_1}\dot{Z_1}-a\dot{I_2}\dot{Z_2}\]
\[=a^2\dot{E_a}-a^2\dot{I_1}\dot{Z_1}+a\dot{I_1}\dot{Z_2}=a^2\dot{E_a}-\dot{I_1}(a^2\dot{Z_1}-a\dot{Z_2})\]
\[=a^2\dot{E_a}-\frac{a^2\dot{Z_1}-a\dot{Z_2}}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}=\frac{\dot{Z_2}(a^2+a)+a^2R}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}=\frac{-\dot{Z_2}+a^2R}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}\]
\(\dot{V_c}\)を求める。
\[\dot{V_c}=\dot{V_0}+a\dot{V_1}+a^2\dot{V_2}=-\dot{I_0}\dot{Z_0}+a\dot{E_a}-a\dot{I_1}\dot{Z_1}-a^2\dot{I_2}\dot{Z_2}\]
\[=a\dot{E_a}-a\dot{I_1}\dot{Z_1}+a^2\dot{I_1}\dot{Z_2}=a\dot{E_a}-\dot{I_1}(a\dot{Z_1}-a^2\dot{Z_2})\]
\[=a\dot{E_a}-\frac{a\dot{Z_1}-a^2\dot{Z_2}}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}=\frac{\dot{Z_2}(a^2+a)+aR}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}=\frac{-\dot{Z_2}+aR}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}\]
まとめると、
\[\dot{V_a}=\frac{2\dot{Z_2}+R}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a} \dot{V_b}=\frac{-\dot{Z_2}+a^2R}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a} \dot{V_c}=\frac{-\dot{Z_2}+aR}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}\]
対称分等価回路
\(\dot{I_0}=0\)、\(\dot{I_1}=-\dot{I_2}\)より、対称分等価回路は以下のようになる。
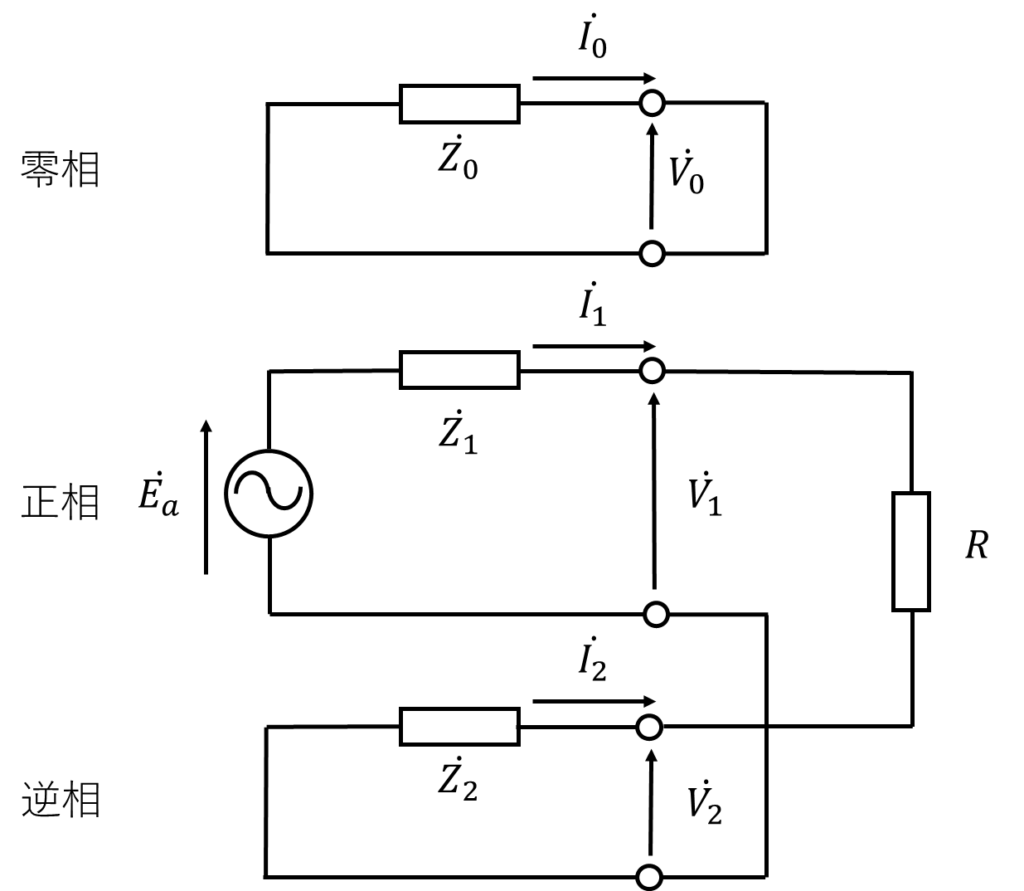
零相回路が短絡され、正相・逆相回路が並列に接続されている。
このため、二相短絡では零相分は考慮しなくてよいことがわかる。
正相電圧、対称分インピーダンスで表した式
導出した式をまとめてみます。
\[\dot{I_b}=-j\frac{\sqrt{3}\dot{E_a}}{\dot{Z_1}+\dot{Z_2}+R}\]
\[\dot{I_c}=j\frac{\sqrt{3}\dot{E_a}}{\dot{Z_1}+\dot{Z_2}+R}\]
\[\dot{V_a}=\frac{2\dot{Z_2}+R}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}\]
\[\dot{V_b}=\frac{-\dot{Z_2}+a^2R}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}\]
\[\dot{V_c}=\frac{-\dot{Z_2}+aR}{\dot{Z_1}+\dot{Z_2}+R}\dot{E_a}\]
まとめ
今回は二相短絡事故を対称座標法を用いた式の導出過程を表してみました!
特に電験一種二次試験ではちょくちょく二相短絡事故の解析が出るので、要チェックな論点になります。
がんばってください!
おわり



コメント