~三相短絡事故~
問題
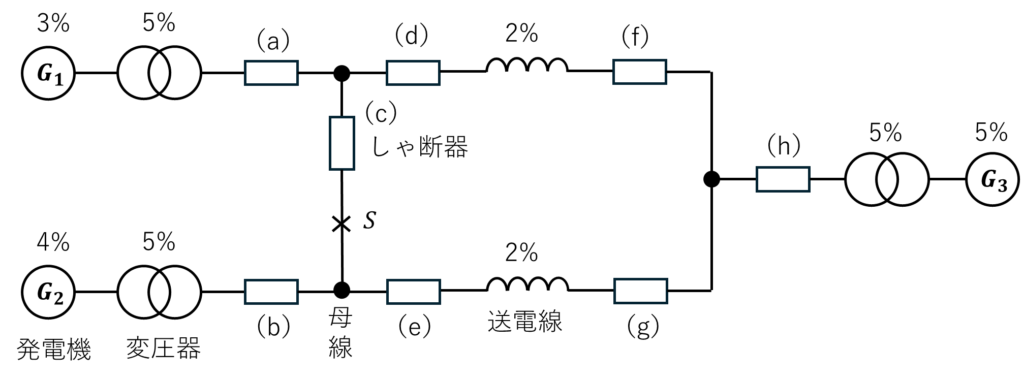
図に示すような3台の発電機\(G_1\)、\(G_2\)及び\(G_3\)で構成された電力系統がある。図中の\(S\)点で三相短絡が発生した場合、\(S\)点に流れる故障電流は、何アンペアとなるか。また、しゃ断器(c)のしゃ断容量は、何キロボルトアンペア以上が必要か。ただし、母線電圧は\(220\)[kV]で、図に示す各部の%インピーダンスは、すべて\(10\)[MV・A]基準に換算したものである。なお、各インピーダンスとも、抵抗分とリアクタンス分の比は等しいものとする。
解答
\(S\)点に流れる故障電流
\[858[A]\]
しゃ断器(c)のしゃ断容量
\[170 000[kV・A]\]
解説
簡略化のため、遮断器を省略し、インピーダンスをリアクタンス分のみと仮定した図を示す。抵抗分とリアクタンス分の比は等しいことから、インピーダンスは代数和で計算できる。
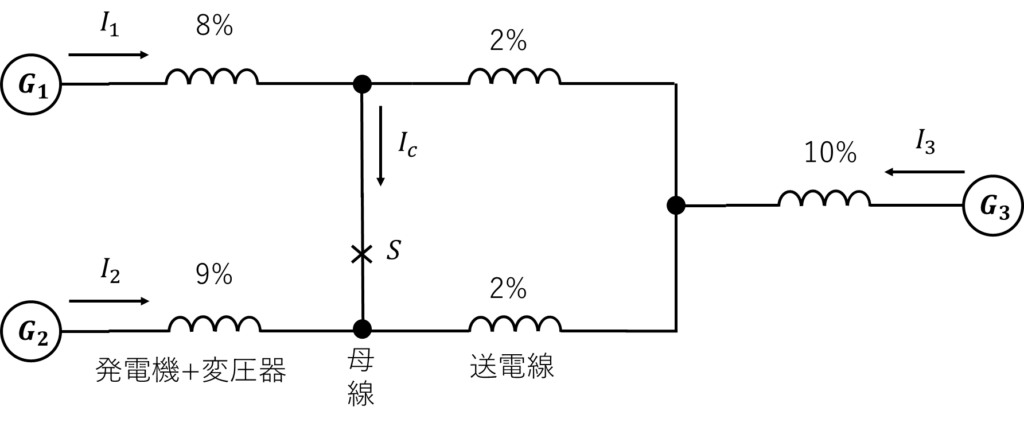
三相短絡点\(S\)の電位は\(0\)[V]となることから、故障電流を計算する。母線での基準電流を\(I_n\)として
\[I_1=\frac{100}{8}I_n=12.5I_n\]
\[I_2=\frac{100}{9}I_n=11.111I_n\]
\[I_3=\frac{100}{10+\frac{2\times 2}{2+2}}I_n=9.09I_n\]
基準電流\(I_n\)は、基準容量\(P_n\)、基準電圧\(V_n\)として
\[I_n=\frac{P_n}{\sqrt{3}V_n}=\frac{10\times 10^6}{\sqrt{3}\times 220\times 10^3}=26.244A\]
事故点を流れる電流\(I_s\)は
\[I_s=I_1+I_2+\frac{I_3}{2}+\frac{I_3}{2}=32.701I_n=858.205\to 858A\]
遮断器(c)を流れる事故電流\(I_c\)は
\[I_c=I_1+\frac{I_3}{2}=17.045I_n=447.329A\]
必要な遮断容量\(P_c\)は
\[P_c=\sqrt{3}V_nI_c=\sqrt{3}\times 200\times 10^3\times 447.329=170450\times 10^3\to 170000[kV・A]\]
出典
昭和54年度第二種電気主任技術者筆記試験発変電問1



コメント