~過渡現象~
問題
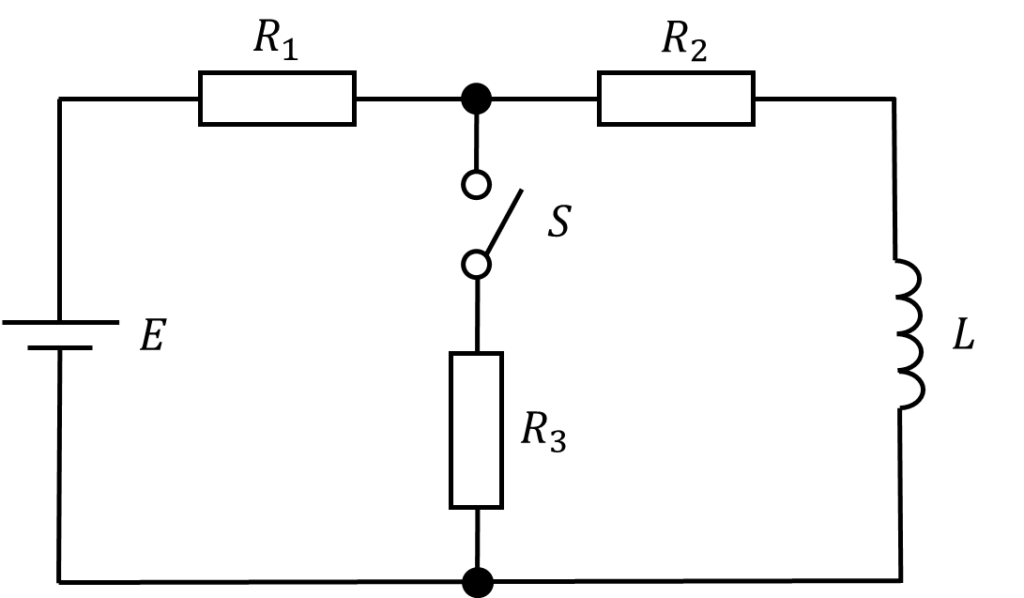
図において、回路が定常状態にあるとき、時刻\(t=0\)においてスイッチ\(S\)を閉じた。次の問に答えよ。
(1)\(t>0\)においてインダクタンスを流れる電流を求めよ。ただし、\(R_1R_2+R_2R_3+R_3R_1=K\)とする。
(2)(1)の電流の過渡項の時定数は、いくらか。
(3)有限の\(R_3\)の値に対して、(1)の電流が、スイッチ\(S\)を閉じても、時間に対して変化しない条件を求めよ。
解答
(1)
\[\frac{E}{K}\left(R_3+\frac{R_1R_2}{R_1+R_2}e^{-\frac{K}{L\left(R_1+R_2\right)}t}\right)\]
(2)
\[\frac{L\left(R_1+R_3\right)}{K}=\frac{L\left(R_1+R_3\right)}{R_1R_2+R_2R_3+R_3R_1}\]
(3)
\(R_1=0\)または\(R_2=0\)
解説
回路に流れる電流を以下のように定義する。
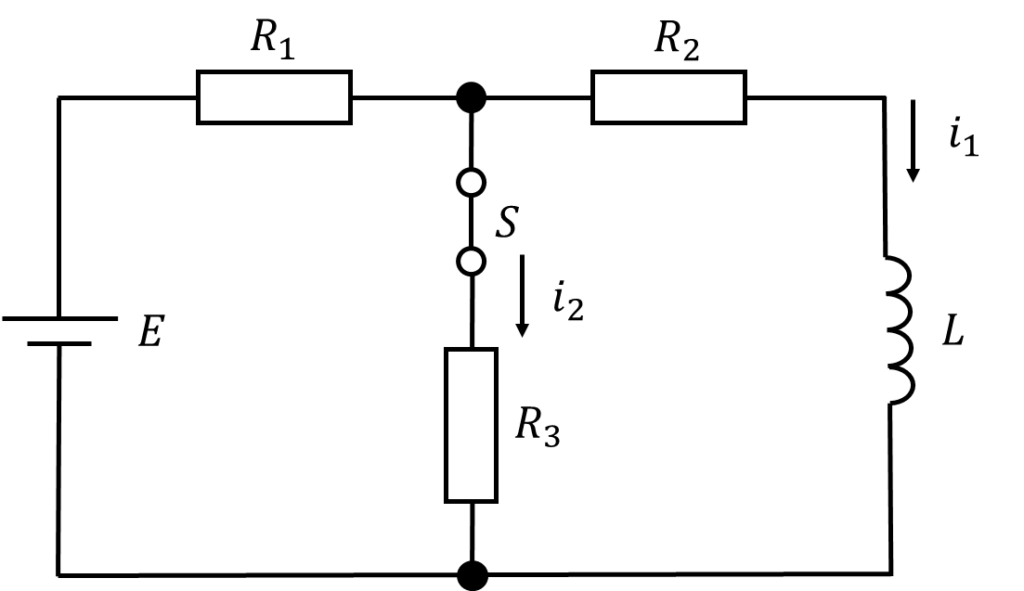
図から、以下の回路方程式が成り立つ。
\[E=R_1\left(i_1(t)+i_2(t)\right)+i_1(t)R_2+L\frac{di_1(t)}{dt}\]
\(i_2(t)\)を消去するため、もう1つの回路方程式を立てる。
\[i_2(t)R_3=i_1(t)R_2+L\frac{di_1(t)}{dt}\]
\(i_2(t)\)を消去し、以下の微分方程式が導出される。
\[E=L\left(1+\frac{R_1}{R_3}\right)\frac{di_1(t)}{dt}+i_1(t)\left(R_1+R_2+\frac{R_1R_2}{R_3}\right)\]
(1)インダクタンスに流れる電流
変数分離による微分方程式の解
\[E=L\left(1+\frac{R_1}{R_3}\right)\frac{di_1(t)}{dt}+i_1(t)\left(R_1+R_2+\frac{R_1R_2}{R_3}\right)\]
定常解\(i_{1s}(t)\)は\(\frac{di_1(t)}{dt}\)が0になっているため
\[E=i_1(t)\left(R_1+R_2+\frac{R_1R_2}{R_3}\right)\to i_1(t)=\frac{E}{R_1+R_2+\frac{R_1R_2}{R_3}}\]
\[=\frac{ER_3}{R_1R_2+R_2R_3+R_3R_1}=\frac{ER_3}{K}\]
過渡解\(i_{1t}(t)\)は、\(E=0\)として
\[L\left(1+\frac{R_1}{R_3}\right)\frac{di_{1t}(t)}{dt}+i_{1t}(t)\left(R_1+R_2+\frac{R_1R_2}{R_3}\right)=0\]
\[\frac{1}{i_{1t}(t)}\frac{di_{1t}(t)}{dt}=-\frac{R_1+R_2+\frac{R_1R_2}{R_3}}{L\left(1+\frac{R_1}{R_3}\right)}=-\frac{R_1R_2+R_2R_3+R_3R_1}{L(R_1+R_3)}=-\frac{K}{L(R_1+R_3)}\]
両辺を\(t\)で積分する。積分定数を\(C\)とする。
\[\int{\frac{1}{i_{1t}(t)}\frac{di_1(t)}{dt}}dt=\int{-\frac{K}{L(R_1+R_3)}}dt\]
\[\ln{i_{1t}(t)}=-\frac{K}{L(R_1+R_3)}t+C\]
ここで\(e^C=A\)とおくと
\[i_{1t}(t)=Ae^{-\frac{K}{L(R_1+R_3)}t}\]
\(i_1(t)\)は\(i_{1s}(t)\)と\(i_{1t}(t)\)の和であることから
\[i_1(t)=\frac{ER_3}{K}+Ae^{-\frac{K}{L(R_1+R_3)}t}\]
初期条件は、\(t=0\)のとき\(i_1(t)=\frac{E}{R_1+R_2}\)より(\(L\)は短絡となっていた)
\[\frac{E}{R_1+R_2}=\frac{ER_3}{K}+A\to A=\frac{E}{R_1+R_2}-\frac{ER_3}{K}\]
\[A=\frac{E}{K}\left(\frac{K}{R_1+R_2}-R_3\right)=\frac{E}{K}\frac{R_1R_2}{R_1+R_2}\]
よって
\[i_1(t)=\frac{ER_3}{K}+\frac{E}{K}\frac{R_1R_2}{R_1+R_2}e^{-\frac{K}{L(R_1+R_3)}t}=\frac{E}{K}\left(R_3+\frac{R_1R_2}{R_1+R_2}e^{-\frac{K}{L(R_1+R_3)}t}\right)\]
ラプラス変換による微分方程式の解
\[E=L\left(1+\frac{R_1}{R_3}\right)\frac{di_1(t)}{dt}+i_1(t)\left(R_1+R_2+\frac{R_1R_2}{R_3}\right)\]
上式をラプラス変換して
\[\frac{E}{s}=L\left(1+\frac{R_1}{R_3}\right)\left(sI_1(s)-i_1(0)\right)+I_1(s)\left(R_1+R_2+\frac{R_1R_2}{R_3}\right)\]
\(i_1(0)=\frac{E}{R_1+R_2}\)より
\[\frac{E}{s}=I_1(s)\left(sL\left(1+\frac{R_1}{R_3}\right)+R_1+R_2+\frac{R_1R_2}{R_3}\right)-L\left(1+\frac{R_1}{R_3}\right)\frac{E}{R_1+R_2}\]
\(I_1(s)\)について解くと
\[I_1(s)=\frac{E}{s\left(sL\left(1+\frac{R_1}{R_3}\right)+R_1+R_2+\frac{R_1R_2}{R_3}\right)}+\frac{EL\left(1+\frac{R_1}{R_3}\right)}{(R_1+R_2)\left(sL\left(1+\frac{R_1}{R_3}\right)+R_1+R_2+\frac{R_1R_2}{R_3}\right)}\]
\(R_1R_2+R_2R_3+R_3R_1=K\)となるように変形して
\[I_1(s)=\frac{ER_3}{s(sL(R_1+R_3)+K)}+\frac{EL(R_1+R_3)}{(R_1+R_2)(sL(R_1+R_3)+K)}\]
\[=\frac{\frac{ER_3}{L(R_1+R_3)}}{s\left(s+\frac{K}{L(R_1+R_3)}\right)}+\frac{E}{(R_1+R_2)\left(s+\frac{K}{L(R_1+R_3)}\right)}\]
第一項を部分分数分解し、ラプラス逆変換できるように変形する。
\[I_1(s)=\frac{ER_3}{K}\left(\frac{1}{s}-\frac{1}{s+\frac{K}{L(R_1+R_3)}}\right)+\frac{E}{(R_1+R_2)\left(s+\frac{K}{L(R_1+R_3)}\right)}\]
ラプラス逆変換して
\[i_1(t)=\frac{ER_3}{K}\left(1-e^{-\frac{K}{L(R_1+R_3)}t}\right)+\frac{E}{R_1+R_2}e^{-\frac{K}{L(R_1+R_3)}t}\]
\[=\frac{E}{K}\left(R_3+\left(\frac{K}{R_1+R_2}-R_3\right)e^{-\frac{K}{L(R_1+R_3)}t}\right)\]
\[=\frac{E}{K}\left(R_3+\frac{R_1R_2}{R_1+R_2}e^{-\frac{K}{L(R_1+R_3)}t}\right)\]
なっが。
(2)時定数
一般的に、過渡項は、定数を\(A\)時定数を\(\tau\)とすると
\[Ae^{-\frac{t}{\tau}}\]
と表される。時定数だけ時間が経過すると、\(A\)の\(36.8\)%に減少することになる。よって、時定数は
\[\tau=\frac{L(R_1+R_3)}{K}=\frac{L(R_1+R_3)}{R_1R_2+R_2R_3+R_3R_1}\]
(3)(1)の電流がスイッチ\(S\)を閉じても時間的に変化しない条件
\[i_1(t)=\frac{E}{K}\left(R_3+\frac{R_1R_2}{R_1+R_2}e^{-\frac{K}{L(R_1+R_3)}t}\right)\]
より、時間に依存するのは第二項のみである。この減衰項の係数は\(\frac{R_1R_2}{R_1+R_2}\)より、\(R_1\)、または\(R_2\)が\(0\)のとき時間に対して無関係になる。
\(R_1\)、\(R_2\)ともに\(0\)のときは短絡なのでマズい。
ちなみに、この時の電流は\(R_1=0\)のとき
\[i_1(t)=\frac{ER_3}{R_2R_3}=\frac{E}{R_2}\]
\(R_2=0\)のとき
\[i_1(t)=\frac{ER_3}{R_3R_1}=\frac{E}{R_1}\]
出典
昭和54年度第二種電気主任技術者筆記試験理論問2



コメント