~環状ソレノイド~
問題
図のような平均半径\(R\)、比透磁率\(\mu_s\)で、断面積\(S_1\)の円形断面をもつ心環に巻いた総巻数\(N_1\)の環状ソレノイドの上に、さらに総巻数\(N_2\)、断面積\(S_2\)の環状ソレノイドを巻いてある。この場合の各ソレノイドの自己インダクタンス\(L_1\)、\(L_2\)及び両者間の相互インダクタンス\(M\)並びに両者間の結合係数\(K\)を求めよ。ただし、心環の断面の半径は\(R\)に比べて非常に小さく、また、巻線1のソレノイドの内部及び巻線1、2間の空間の磁束密度はそれぞれ一様で、漏れ磁束はないものとし、なお、空間の比透磁率を1、真空の透磁率を\(\mu_0\)とする。
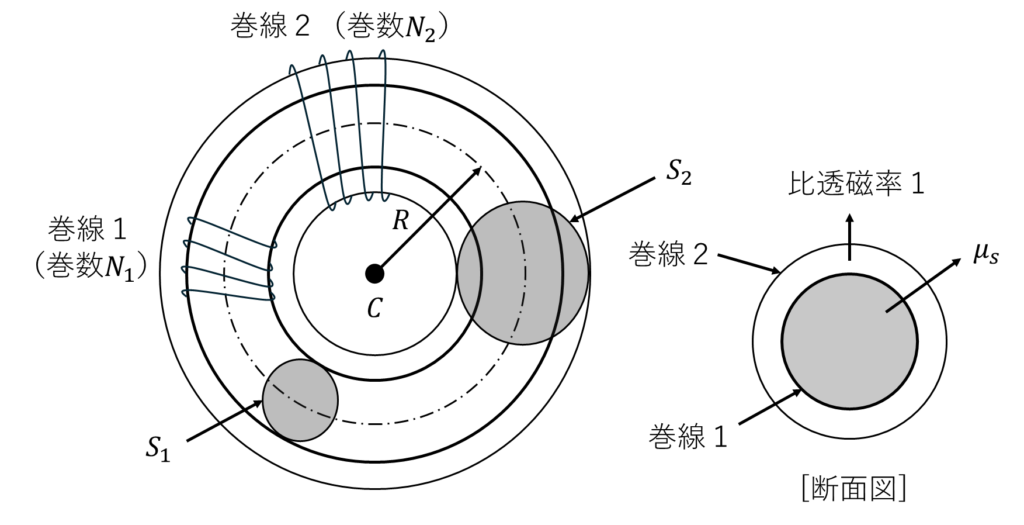
解答
\[L_1=\frac{\mu_0\mu_sS_1N_1^2}{2\pi R}\]
\[L_2=\frac{(\mu_0(\mu_s-1)S_1+S_2)N_2^2}{2\pi R}\]
\[M=\frac{\mu_0\mu_sS_1N_1N_2}{2\pi R}\]
\[K=\sqrt{\frac{\mu_sS_1}{(\mu_s-1)S_1+S_2}}\]
解説
\(L_1\)
巻線1にのみ電流\(I_1\)を流すとき、断面積\(S_1\)の心環中を通る磁束\(\phi_1\)は、起磁力\(F_{m1}\)、磁気抵抗\(R_{m1}\)とすると
\[F_{m1}=N_1I_1 R_{m1}=\frac{2\pi R}{\mu_0 \mu_s S_1}\]
となることから、
\[\phi_1=\frac{F_{m1}}{R_{m1}}=\frac{N_1I_1}{\frac{2\pi R}{\mu_0 \mu_s S_1}}=\frac{\mu_0 \mu_s N_1I_1S_1}{2\pi R}\]
巻線1の自己インダクタンス\(L_1\)は
\[L_1=\frac{N_1\phi_1}{I_1}=\frac{\mu_0 \mu_s S_1N_1^2}{2\pi R}\]
\(L_2\)
巻線2のみに電流\(I_2\)を流すとき、断面積\(S_2\)の心環中を通る磁束\(\phi_2\)は起磁力\(F_{m2}\)、磁気抵抗\(R_{m2}\)とすると
\[F_{m2}=N_2I_2\]
ここで\(R_{m2}\)は下図の赤色と青色の領域の磁気抵抗の並列であることから、
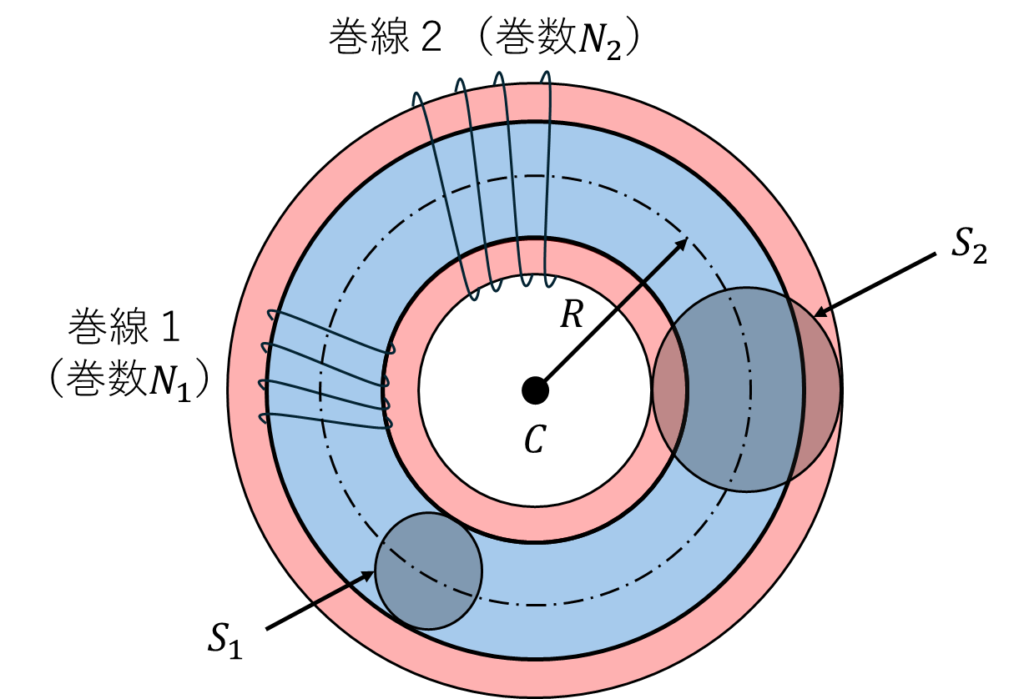
\[R_{m2}=\frac{1}{\frac{\mu_0 \mu_s S_1}{2\pi R}+\frac{\mu_0(S_2-S_1)}{2\pi R}}=\frac{2\pi R}{\mu_0\left((\mu_s-1)S_1+S_2\right)}\]
よって
\[\phi_2=\frac{F_{m2}}{R_{m2}}=\frac{\mu_0 N_2I_2(\left(\mu_s-1\right)S_1+S_2)}{2\pi R}\]
巻線2の自己インダクタンス\(L_2\)は
\[L_2=\frac{N_2\phi_2}{I_2}=\frac{\mu_0 N_2^2(\left(\mu_s-1\right)S_1+S_2)}{2\pi R}\]
\(M\)
2通りの求め方があるので、それぞれ紹介する。
巻線1による磁束\(\phi_1\)が巻線2に鎖交
\(\phi_1\)はそのすべてが巻線2に鎖交する。よって、相互インダクタンス\(M\)は
\[M=\frac{N_2\phi_1}{I_1}=\frac{\mu_0 \mu_s N_1N_2S_1}{2\pi R}\]
巻線2による磁束\(\phi_2\)が巻線1に鎖交
\(\phi_2\)は、一部が巻線1と鎖交する。巻線1と鎖交する磁束を\(\phi_{2\to 1}\)とすると
\[\phi_{2\to 1}=\frac{\frac{2\pi R}{\mu_0(S_2-S_1)}}{\frac{2\pi R}{\mu_0 \mu_s S_1}+\frac{2\pi R}{\mu_0(S_2-S_1)}}\phi_2=\frac{\mu_0 \mu_s N_2I_2S_1}{2\pi R}\]
よって、相互インダクタンス\(M\)は
\[M=\frac{N_1 \phi_{2\to 1}}{I_2}=\frac{\mu_0 \mu_s N_1N_2S_1}{2\pi R}\]
\(k\)
結合係数\(k\)は
\[M=k\sqrt{L_1L_2}\to k=\frac{M}{\sqrt{L_1L_2}}=\sqrt{\frac{\mu_sS_1}{(\mu_s-1)S_1+S_2}}\]
出典
昭和54年度第二種電気主任技術者筆記試験理論問1



コメント