~物質中の損失、発光ダイオード、電圧実効値・波形率・波高率の複合問題~
問題
次の\(\boxed{ }\)の中に適当な答を記入せよ。
(1)通電中の金属導体では、\(\boxed{ }\)と格子原子との衝突による\(\boxed{ }\)損が発生するが、誘電体では、交流電界のもとで誘電分極の遅れに伴う\(\boxed{ }\)損が存在する。強磁性体では、交流磁界のもとで\(\boxed{ }\)損と\(\boxed{ }\)損が発生する。後者は、通電中の金属導体中での損失と同じ原理に基づくものである。
(2)発光ダイオードは、半導体中につくられたpn接合の\(\boxed{ }\)方向に電圧を加え、p側に\(\boxed{ }\)、n側に\(\boxed{ }\)の少数キャリアを注入し、その\(\boxed{ }\)によって発生するエネルギー放出、すなわち光を用いるもので、半導体材料の物理的性質によって、発光\(\boxed{ }\)は決定される。
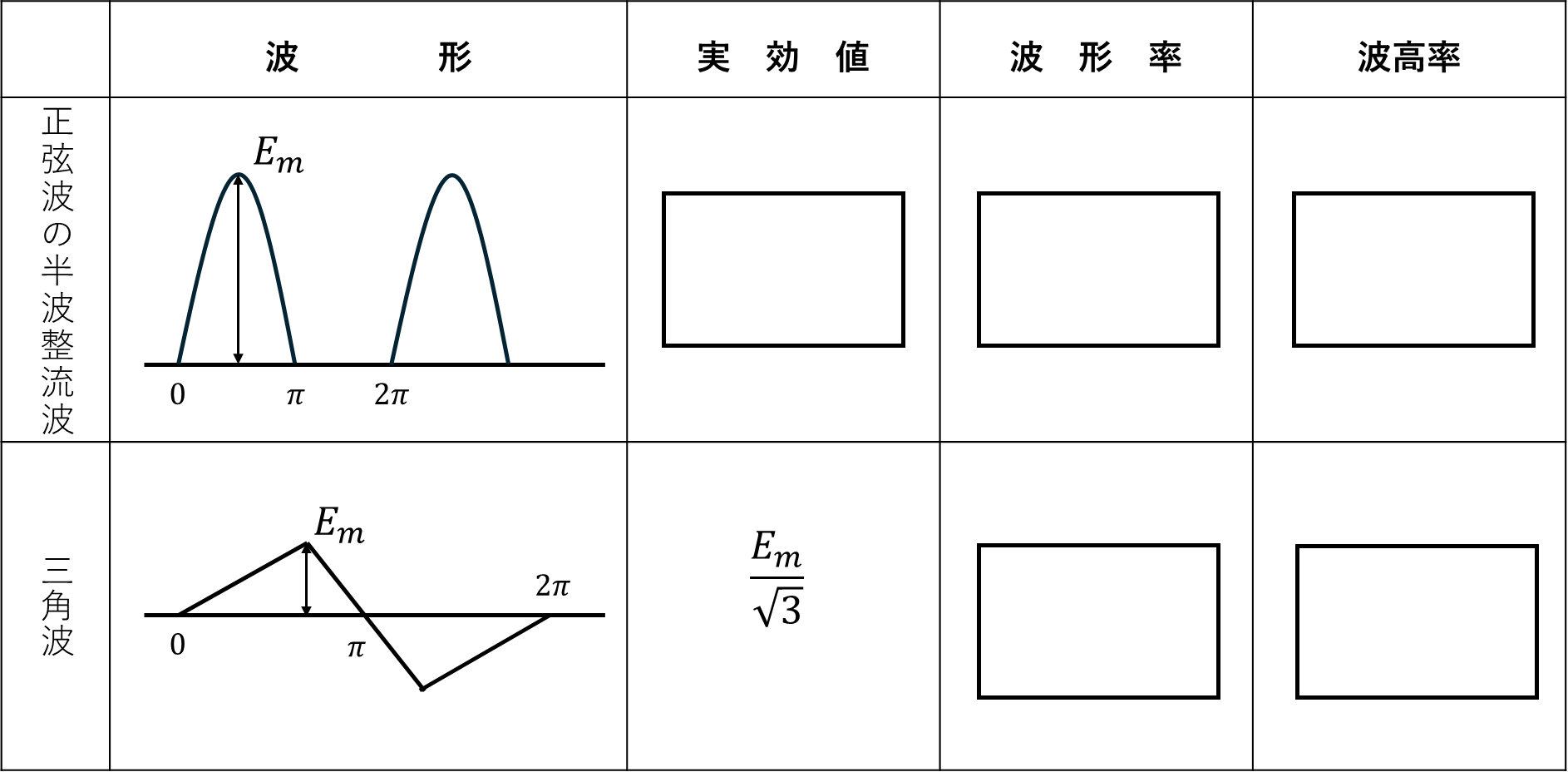
(3)次の表は、図示の波形を有する電圧の実効値、波形率及び波高率を示したものである。
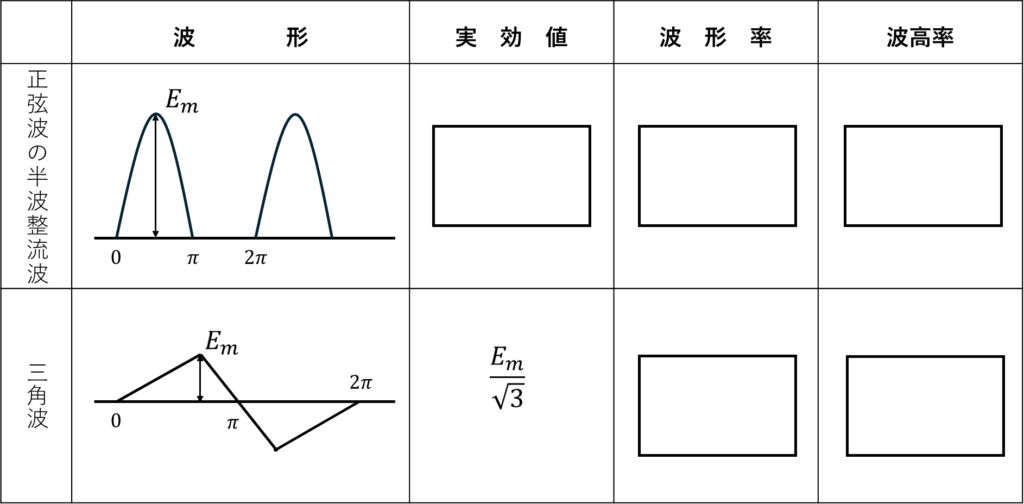
解説
(1)通電中の金属導体では、電子と格子原子との衝突による抵抗損が発生するが、誘電体では、交流電界のもとで誘電分極の遅れに伴う誘電損が存在する。強磁性体では、交流磁界のもとでヒステリシス損と渦電流損が発生する。後者は、通電中の金属導体中での損失と同じ原理に基づくものである。
(2)発光ダイオードは、半導体中につくられたpn接合の順方向に電圧を加え、p側に電子、n側に正孔の少数キャリアを注入し、その再結合によって発生するエネルギー放出、すなわち光を用いるもので、半導体材料の物理的性質によって、発光波長は決定される。
(3)
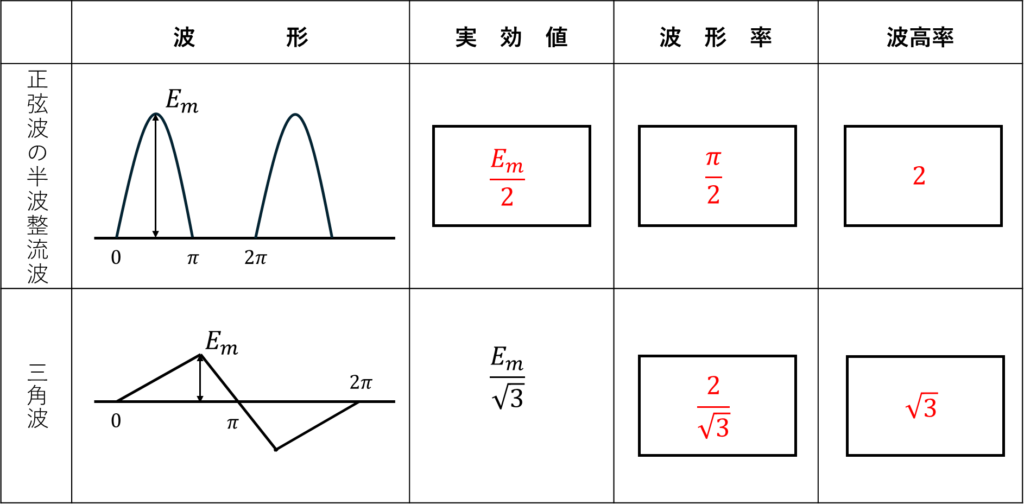
\[波形率=\frac{実効値}{平均値} 波高率=\frac{最大値}{実効値}\]
と定義される。最大値がわかっていることから、それぞれの波形について平均値、実効値を求める。
正弦波の半波整流波
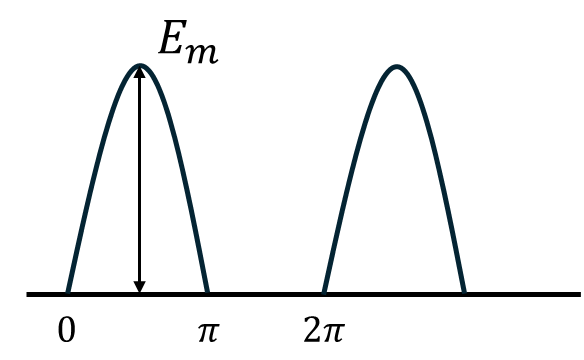
半周期の波形は以下の式で表されるとする。
\[e=E_m\sin{\theta}\]
ここで、平均値\(E_a\)は、半周期でのグラフの面積を底辺(\(2\pi\))で除したものとなる。
グラフの面積を、一辺を\(2\pi\)として均したものといえる。
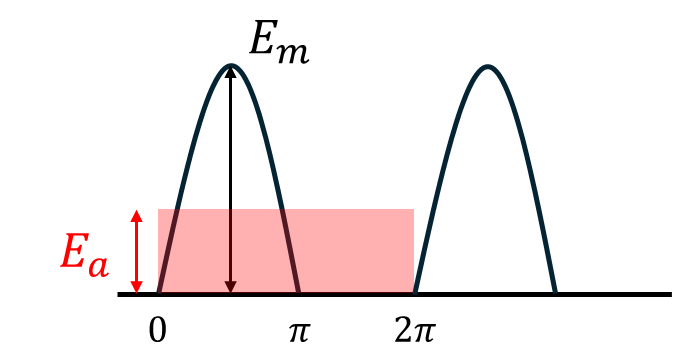
\[E_a=\frac{1}{2\pi}\int^{\pi}_{0}{ed\theta}=\frac{E_m}{2\pi}\int^{\pi}_{0}{\sin{\theta}d\theta}\]
\[=\frac{E_m}{2\pi}\left[-\cos{\theta}\right]^{\pi}_{0}=\frac{E_m}{2\pi}\left(1+1\right)=\frac{E_m}{\pi}\]
実効値\(E\)は
\[E=\sqrt{\frac{1}{2\pi}\int^{\pi}_{0}{e^2d\theta}}=\sqrt{\frac{E_m^2}{2\pi}\int^{\pi}_{0}{\sin^2\theta d\theta}}\]
\[=\sqrt{\frac{E_m^2}{2\pi}\int^{\pi}_{0}{\frac{1-\cos{(2\theta)}}{2}}d\theta}=\sqrt{\frac{E_m^2}{2\pi}\left[\frac{1}{2}\theta-\frac{1}{4}\sin{(2\theta)}\right]^{\pi}_{0}}\]
\[=\sqrt{\frac{E_m^2}{2\pi}\left(\frac{\pi}{2}-0-0+0\right)}=\sqrt{\frac{E_m^2}{4}}=\frac{E_m}{2}\]
波形率は
\[波形率=\frac{実効値}{平均値}=\frac{\frac{E_m}{2}}{\frac{E_m}{\pi}}=\frac{\pi}{2}\]
波高率は
\[波高率=\frac{最大値}{実効値}=\frac{E_m}{\frac{E_m}{2}}=2\]
三角波
三角波の考え方を図に示す。
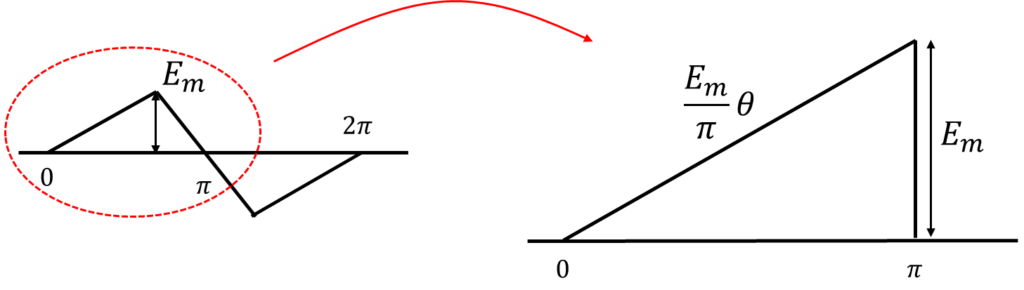
三角波の最大値をずらし、等積変形する。
平均値\(E_a\)は、半周期の面積が\(\frac{1}{2}\pi E_m\)より、
\[E_a=\frac{\frac{1}{2}\pi E_m}{\pi}=\frac{E_m}{2}\]
と、瞬殺です。小学生で習う三角形の面積の公式ですね。
斜辺の傾きは\(\frac{E_m}{\pi}\theta\)より、実効値\(E\)は
\[E=\sqrt{\frac{1}{\pi}\int^{\pi}_{0}{\left(\frac{E_m}{\pi}\theta\right)^2}d\theta}=\sqrt{\frac{E_m^2}{\pi^3}\left[\frac{1}{3}\theta^3\right]^{\pi}_{0}}=\sqrt{\frac{E_m^2}{3}}=\frac{E_m}{\sqrt{3}}\]
\(\int\)の先頭が\(\frac{1}{\pi}\)なのは、半波整流と異なり、半周期後も対称な波形が現れているからである。積分範囲が\(0\to \pi\)なのも同様。
波形率は
\[波形率=\frac{実効値}{平均値}=\frac{\frac{E_m}{\sqrt{3}}}{\frac{E_m}{2}}=\frac{2}{\sqrt{3}}\]
波高率は
\[波高率=\frac{最大値}{実効値}=\frac{E_m}{\frac{E_m}{\sqrt{3}}}=\sqrt{3}\]
出典
昭和55年度第二種電気主任技術者筆記試験理論問3



コメント