~直流電動機~
問題
定格電圧\(200\)[V]、定格出力\(45\)[kW]の他励直流電動機がある。この電動機を定格電圧で運転したとき、回転速度は\(900\)[min\(^{-1}\)]、電機子電流は\(270\)[A]であった。励磁電流を一定に保ち、回転速度を\(600\)[min\(^{-1}\)]にするための電動機端子電圧[V]を求めよ。ただし、負荷トルクは速度の2乗に比例するものとし、また、電機子抵抗は\(0.04\)[Ω]、ブラシの電圧降下は\(3\)[V]とし、電機子反作用は無視する。
解答
\(132\)[V]
解説
問題の条件を図に示す。
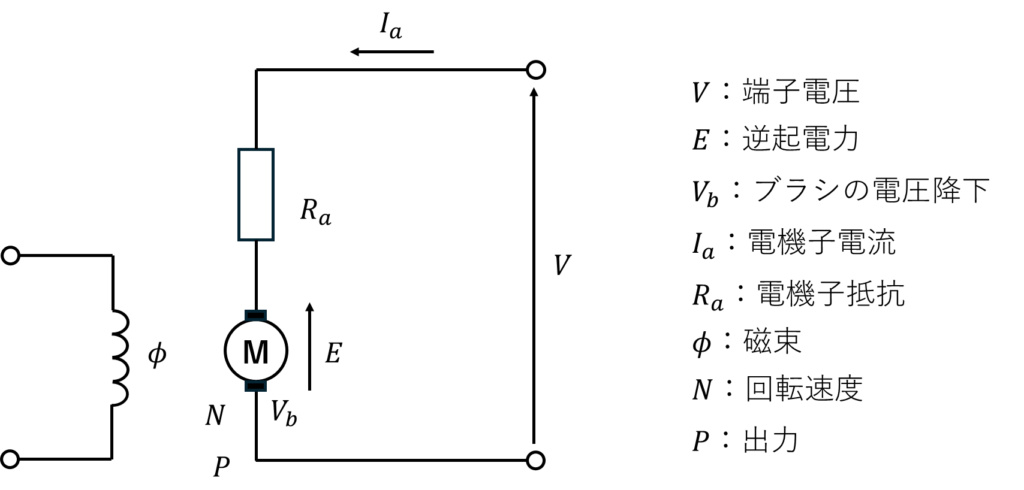
定格運転時の逆起電力\(E\)を求める。
\[E=V-I_aR_a-V_b=200-270\times 0.04-3=186.2\]
逆起電力は、磁束\(\phi\)が一定のとき、回転速度\(N\)に比例することから、回転速度変更後の逆起電力\(E’\)は
\[E’=\frac{N’}{N}E=\frac{600}{900}\times 186.2=124.1333\]
これによって電機子電流\(I_a\)も変化する。電動機のトルク\(T\)は問題条件より回転速度の2乗に比例すること、磁束が一定のとき電機子電流に比例することから
\[\frac{T’}{T}=\frac{I_a’}{I_a}=\left(\frac{N’}{N}\right)^2\to I_a’=\left(\frac{N’}{N}\right)^2I_a=\left(\frac{600}{900}\right)^2\times 270=120\]
回転速度を\(600\)[min\(^{-1}\)]に保つ端子電圧\(V’\)は
\[V’=E’+I_a’R_a+V_b=124.1333+120\times 0.04+3=131.9333\to 132\]
出典
昭和55年度第二種電気主任技術者筆記試験機械問1



コメント