~架空送電線のたるみ~
問題
径間\(300\)[m]のところに張られた架空送電線がある。そのたるみを冬に測ったところ、気温\(-10\)[℃]、無風・無氷雪状態で\(6\)[m]であった。このとき、水平張力はいくらであったか。また、夏において、気温\(35\)[℃]、風のない時には、この電線たるみ及び水平張力はどのように変わるか。ただし、電線\(1\)[m]当たりの重量は\(1.32\)[kg]、温度による線膨張係数は\(1\)[℃]につき\(0.000019\)とし、張力による電線の伸長は無視するものとする。
解説
たるみの差は\(2.06\)[m]
水平張力の差は\(-631\)[N]
解説
問題の条件を図に示す。
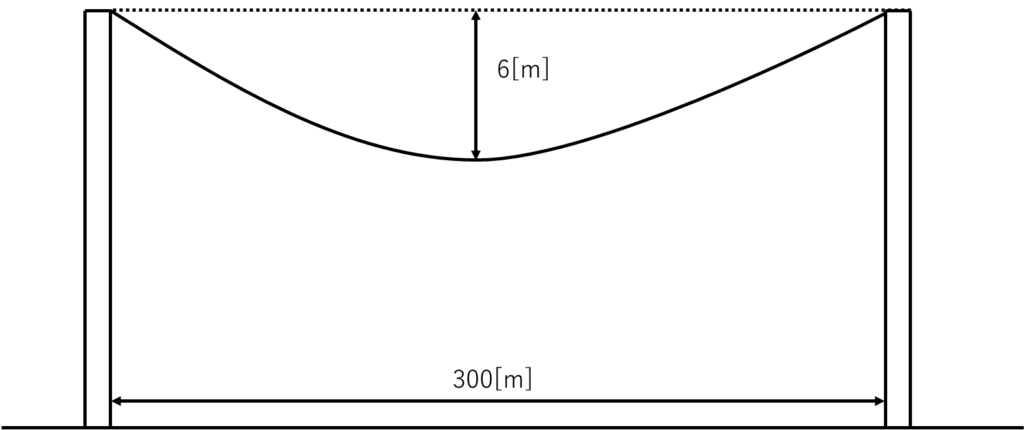
冬季
径間を\(S\)[m]、単位長あたりの電線の重量を\(W\)[kg/m\(^2\)]、水平張力を\(T\)[N]とすると、電線のたるみ\(D\)[m]は
\[D=\frac{WS^2}{8T}\]
よって、張力は
\(T=\frac{WS^2}{8D}=\frac{1.32\times 300^2}{8\times 6}=2475\)[N]
また、電線長\(L\)[m]は
\(L=S+\frac{8D^2}{3S}=300+\frac{8\times 6^2}{3\times 300}=300.32\)[m]
夏季
夏季においては、冬季との温度差が\(45\)[℃]であることから、電線長\(L’\)は
\(L’=300.32(1+0.000019\times 45)=300.57677\)[m]
新たなたるみ\(D’\)は、
\(D’=\sqrt{\frac{3S}{8}(L’-S)}=\sqrt{\frac{3\times 300}{8}(300.57677-300)}=8.05522\)
冬季との差は、
\(D’-D=8.05522-6=2.05522\to 2.06\)[m]
水平張力は
\(T’=\frac{WS^2}{8D’}=\frac{1.32\times 300^2}{8\times 8.05522}=1843.525\)[m]
冬季との差は
\(T’-T=1843.525-2475=-631.475\to -631\)[N]
出典
昭和60年度第二種電気主任技術者筆記試験送配電問1



コメント