~四端子定数~
問題
公称電圧\(110\)[kV]のある送電線路の四端子定数は、\(\dot{A}=0.98\)、\(\dot{B}=j70.7\)[Ω]、\(\dot{C}=j0.56\times 10^{-3}\)[S]及び\(\dot{D}=0.98\)である。受電端電圧が\(100\)[kV]で、受電端負荷が遅れ力率\(80\)[%]の\(21\)[MW]であるとき、送電端電圧[kV]を求めよ。
解答
\(110\)[kV]
解説
問題の条件を図に示す。
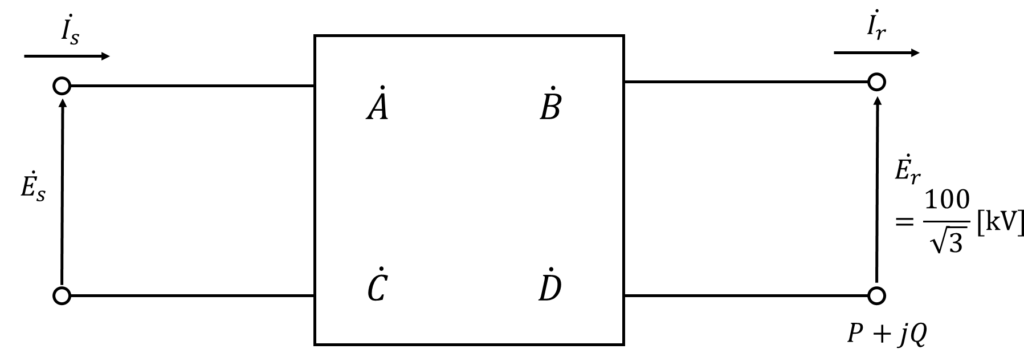
線間電圧を\(\dot{V}\)、相電圧を\(\dot{E}\)としている。
負荷が消費する電力を\(P+jQ\)とすると、
\(P+jQ=21+\frac{\sqrt{1^2-0.8^2}}{0.8}\times 21=21+j15.75\)[Mvar]
負荷に流れ込む電流\(\dot{I_r}\)は
\(\dot{I_r}=\frac{\overline{P+jQ}}{\sqrt{3}\dot{V_r}}=\frac{P-jQ}{\sqrt{3}\dot{V_r}}\)
\(=\frac{21-15.75}{\sqrt{3}\times 100\times10^3}\times 10^6=121.24356-j90.9327\)[A]
ここで、四端子定数は
\[\begin{bmatrix}\dot{E_s}\\ \dot{I_s}\\ \end{bmatrix}=\begin{bmatrix}\dot{A}&\dot{B}\\ \dot{C}&\dot{D}\\ \end{bmatrix}\begin{bmatrix}\dot{E_r}\\ \dot{I_r}\\ \end{bmatrix}\]
と定義される。よって、送電端の相電圧は
\(\dot{E_s}=\dot{A}\dot{E_r}+\dot{B}\dot{I_r}\)
\(=0.98\times \frac{100}{\sqrt{3}}\times 10^3+j70.7\times(121.24356-j90.9327)\)
\(=63.01+j8.572\)[kV]
これを線間電圧に直すと
\(\dot{V_s}=\sqrt{3}\dot{E_s}=\sqrt{3}\times(63.01+j8.572)\)
\(=109.1333+j14.8467\)[kV]
大きさは
\(V_s=\sqrt{109.1333^2+14.8467^2}=110.14\to 110\)[kV]
出典
昭和60年度第二種電気主任技術者筆記試験送配電問2



コメント