~コンデンサの計算~
問題
図に示すように、間隔\(d\)の平行平板電極がある。両極間は、厚さがそれぞれ\(d_1\)及び\(d_2\)の2種類の導電性誘電体(導電率\(g_1\)及び\(g_2\)、誘電率\(\varepsilon_1\)及び\(\varepsilon_2\))で満たされている。電極間に図のように直流電圧\(V_0\)を加えたときの誘電体境界面の電位及びそこに現れる面電荷密度を求めよ。ただし、平行平板電極は無限に広いとみなし、端効果は無視するものとする。
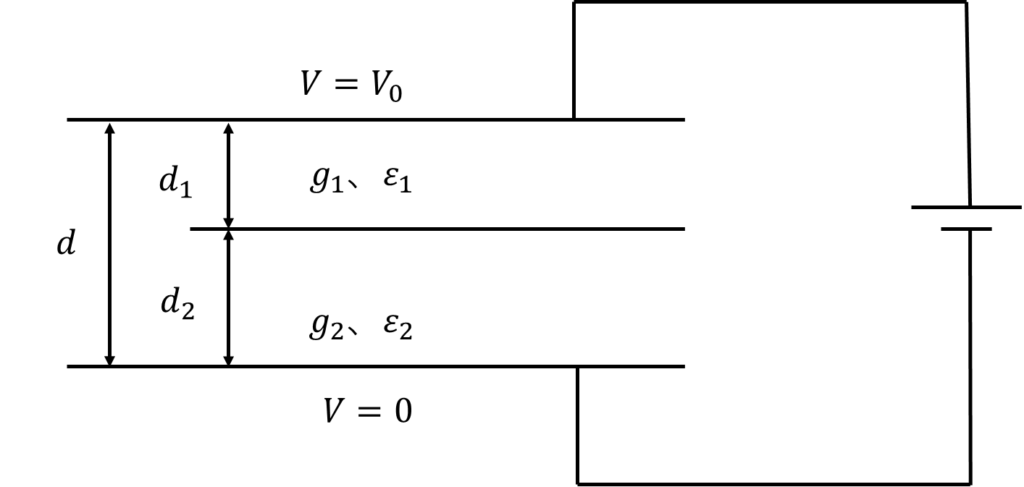
解答
誘電体境界面の電位は
\[\frac{d_2g_1}{d_1g_2+d_2g_1}V_0\]
誘電体境界面の面電荷密度は
\[\frac{\varepsilon_2 g_1-\varepsilon_1 g_2}{d_1g_2+d_2g_1}V_0\]
解説
解説1
極板面積を\(S\)と仮定し、このような等価回路に変換する。
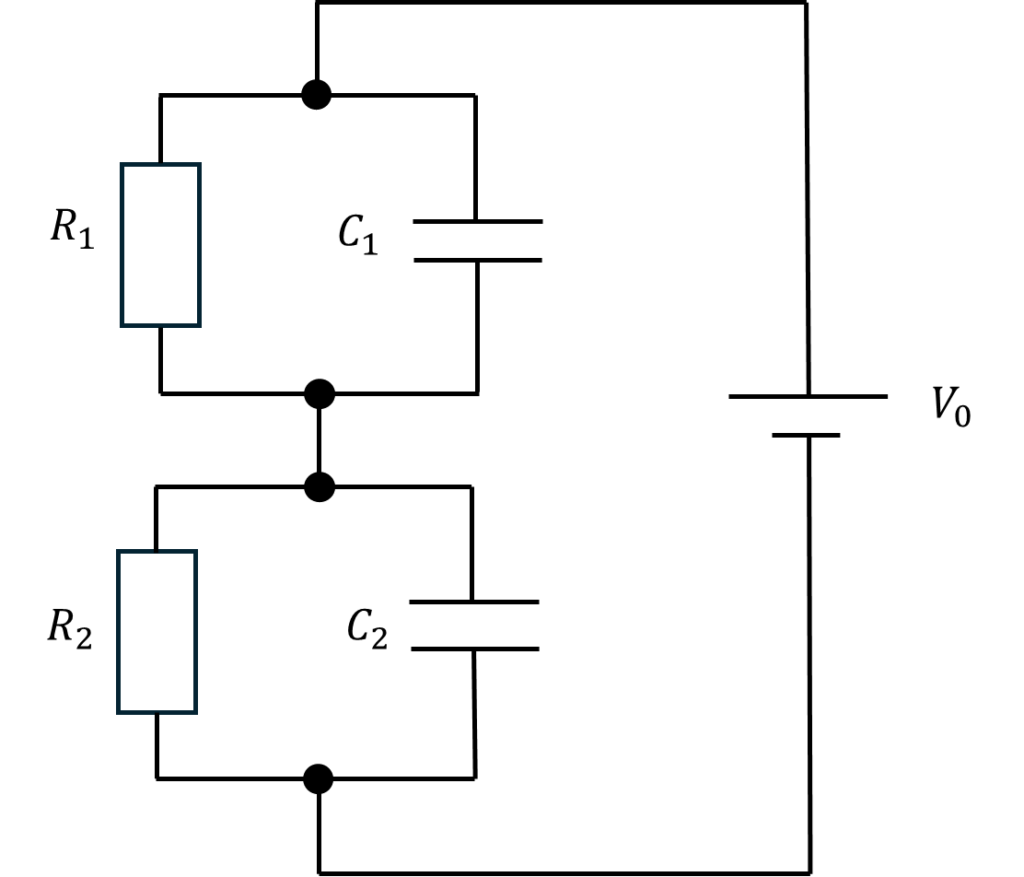
ここで、それぞれの素子は
\[R_1=\frac{1}{g_1}\frac{d_1}{S} R_2=\frac{1}{g_2}\frac{d_2}{S}\]
\[C_1=\frac{\varepsilon_1 S}{d_1} C_2=\frac{\varepsilon_2 S}{d_2}\]
で表される。
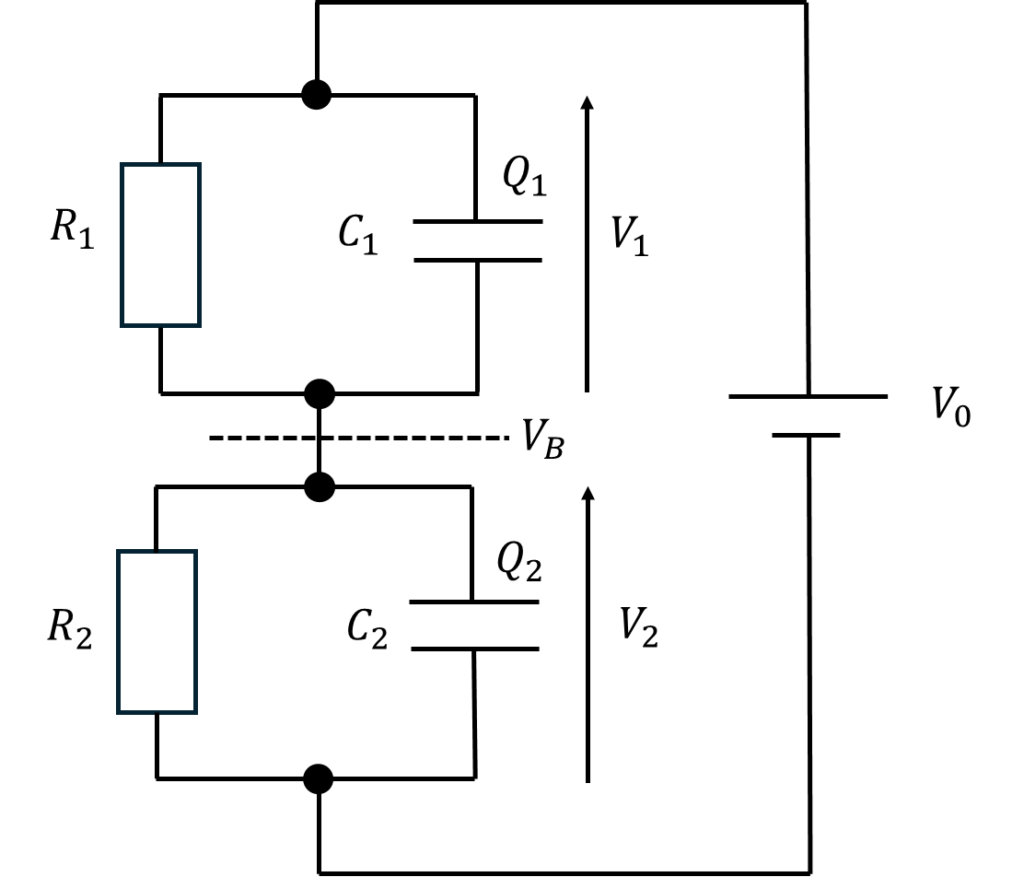
誘電体境界面の電位\(V_B\)は、\(R_1\)と\(R_2\)によって分圧されていると考えられる。
\[V_B=\frac{R_2}{R_1+R_2}V_0=\frac{R_2=\frac{1}{g_2}\frac{d_2}{S}}{\frac{1}{g_1}\frac{d_1}{S}+R_2=\frac{1}{g_2}\frac{d_2}{S}}=\frac{d_2g_1}{d_1g_2+d_2g_1}V_0\]
\(V_1\)は、
\[V_1=V_0-V_2=\frac{d_1g_2}{d_1g_2+d_2g_1}\]
誘電体境界面の面電荷密度\(\sigma\)は、\(C_2\)に蓄えられる正電荷\(Q_2\)と\(C_1\)に蓄えられる負電荷\(Q_1\)の差\(Q_2-Q_1\)を面積\(S\)で除した値である。
\[Q_1=C_1V_1=\frac{\varepsilon_1 S}{d_1}\times \frac{d_1g_2}{d_1g_2+d_2g_1}=\frac{\varepsilon_1 g_2S}{d_1g_2+d_2g_1}V_0\]
\[Q_2=C_2V_2=\frac{\varepsilon_2 S}{d_2}\times \frac{d_2g_1}{d_1g_2+d_2g_1}=\frac{\varepsilon_2 g_1S}{d_1g_2+d_2g_1}V_0\]
\[\sigma=\frac{Q_2-Q_1}{S}=\frac{\varepsilon_2 g_1-\varepsilon_1 g_2}{d_1g_2+d_2g_1}V_0\]
解説2
導電性誘電体の電界をそれぞれ\(E_1\)、\(E_2\)とする。
ここで、方程式をたてる。
\(V=Ed\)より、
\[V_0=E_1d_1+E_2d_2\]
電流密度\(J=gE\)であることから、電流密度の連続性より
\[g_1E_1=g_2E_2\]
\(E_2=\frac{g_1}{g_2}E_1\)より、
\[V_0=E_1(d_1+\frac{g_1}{g_2}d_2)\]
\(E_1\)について解くと
\[E_1=\frac{V_0}{d_1+\frac{g_1}{g_2}d_2}=\frac{g_2}{d_1g_2+d_2g_1}V_0\]
\(E_2=\frac{g_1}{g_2}E_1\)より、
\[E_2=\frac{g_1}{d_1g_2+d_2g_1}V_0\]
誘電体境界面の電位は
\[V_B=E_2d_2=\frac{d_2g_1}{d_1g_2+d_2g_1}V_0\]
電束密度\(D\)と面電荷密度は等しく、\(D=\varepsilon E\)より、
\[D_1=\varepsilon_1 E_1=\frac{\varepsilon_1 g_2}{d_1g_2+d_2g_1}V_0\]
\[D_2=\varepsilon_2 E_2=\frac{\varepsilon_2 g_1}{d_1g_2+d_2g_1}V_0\]
面電荷密度は\(D_2-D_1\)より、
\[\sigma=D_2-D_1=\frac{\varepsilon_2 g_1-\varepsilon_1 g_2}{d_1g_2+d_2g_1}V_0\]
出典
昭和56年度第二種電気主任技術者筆記試験理論問1



コメント