~交流回路のインピーダンス~
問題
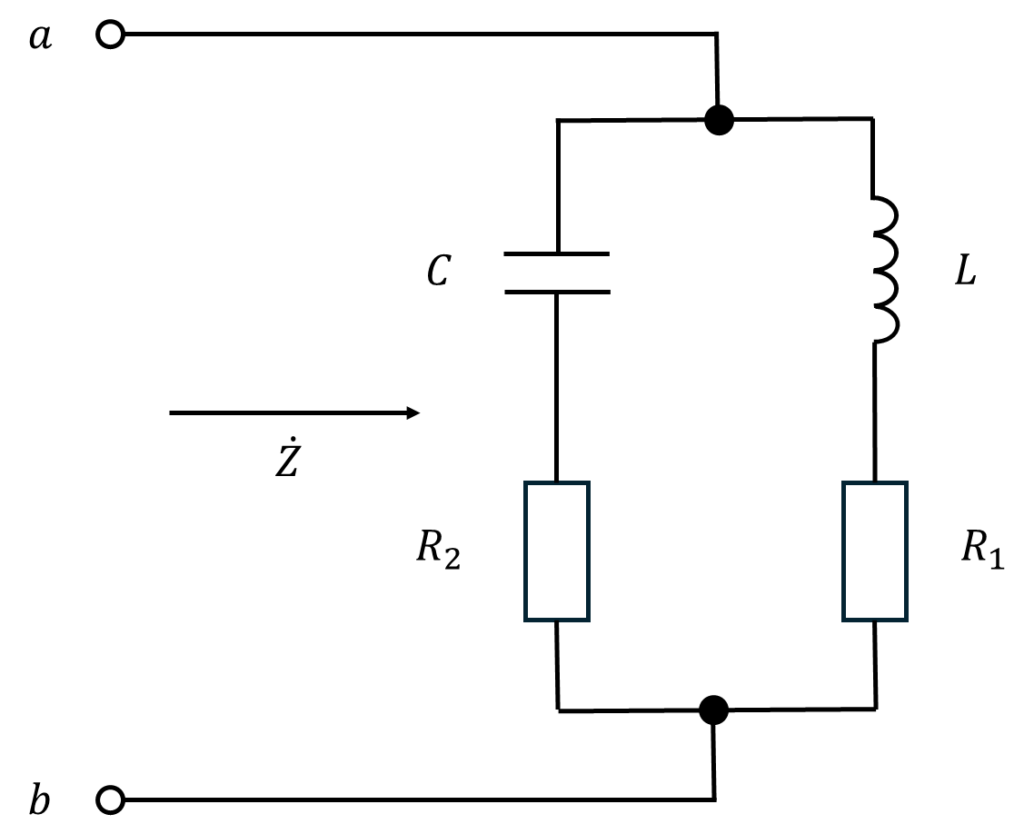
図のように二端子回路の端子\(a\)、\(b\)からみたインピーダンス\(\dot{Z}\)が周波数に無関係に一定であるための条件を求めよ。
解答
\(\dot{Z}\)が周波数に無関係になる条件は
\[R_1=R_2=\sqrt{\frac{L}{C}}\]
解説
各周波数を\(\omega\)としたときのインピーダンスを求める。
\[\dot{Z}=\frac{(R_1+j\omega L)(R_2+\frac{1}{j\omega C})}{(R_1+j\omega L)+(R_2+\frac{1}{j\omega C})}\]
\[=\frac{R_1R_2+\frac{L}{C}+j(\omega LR_2-\frac{R_1}{\omega C})}{R_1+R_2+j(\omega L-\frac{1}{\omega C})}\]
\(\dot{Z}\)が周波数に無関係となるためには、\(\dot{Z}\)の虚部が\(0\)であり、実部が一定である必要がある。
この定数を\(\dot{Z}=k\)とおくと、
\[k=\frac{R_1R_2+\frac{L}{C}+j(\omega LR_2-\frac{R_1}{\omega C})}{R_1+R_2+j(\omega L-\frac{1}{\omega C})}\]
ここで、次の2式が成立する。
\[R_1R_2+\frac{L}{C}=k(R_1+R_2)\]
\[\omega LR_2-\frac{R_1}{\omega C}=k(\omega L-\frac{1}{\omega C})\]
上式より、
\[\omega L(R_2-k)=\frac{1}{\omega C}(R_1-k)\]
周波数に無関係になるためには、
\[R_2=k R_1=k\]
を同時に満たす必要がある。
これを\(R_1R_2+\frac{L}{C}=k(R_1+R_2)\)に代入すると、
\[k^2+\frac{L}{C}=2k^2\]
\[k=\sqrt{\frac{L}{C}}\]
以上より、
\[k=R_1=R_2=\sqrt{\frac{L}{C}}\]
出典
昭和56年度第二種電気主任技術者筆記試験理論問2



コメント