~静電界、高調波、電気計測の複合問題~
問題
次の\(\boxed{ }\)の中に適当な答を記入せよ。
(1)静電界中の、誘電体(誘電率\(\varepsilon\)[F/m])と面電荷密度\(\sigma\)[C/m\(^2\)]が誘導されている導体との界面において、電界の強さは、導体内部では\(\boxed{ }\)であり、誘電体中では\(\boxed{ }\)[V/m]である。また、この界面では、導体に\(\boxed{ }\)[N/m\(^2\)]なる力が\(\boxed{ }\)の向きに働き、誘電体中には\(\boxed{ }\)[J/m\(^3\)]なる電界エネルギーが貯えられている。
(2)各相における大きさが等しく、また、基本波に対して同じ位相関係をもつ高調波の存在する三相回路においては、周波数が\(3n\)倍の高調波は、各相\(\boxed{ }\)である。したがって、これらの高調波は、\(\boxed{ }\)結線回路では、その各相電圧には存在するが、\(\boxed{ }\)電圧には現れない。一方、\(\boxed{ }\)結線回路では、その結線中には、大きさが\(\boxed{ }\)倍の高調波電圧が生じ、循環電流が流れる。
(3)静電形計器は、2枚の電極の間の静電力を利用したもので、\(\boxed{ }\)が極めて少ないから、\(\boxed{ }\)・\(\boxed{ }\)回路の電圧測定に適し、また、周波数特性が優れているので、\(\boxed{ }\)から高調波まで測定可能であり、指示は\(\boxed{ }\)値を示す。
解説
静電界
(1)静電界中の、誘電体(誘電率\(\varepsilon\)[F/m])と面電荷密度\(\sigma\)[C/m\(^2\)]が誘導されている導体との界面において、電界の強さは、導体内部では零であり、誘電体中では\(\frac{\sigma}{\varepsilon}\)[V/m]である。また、この界面では、導体に\(\frac{\sigma^2}{2\varepsilon}\)[N/m\(^2\)]なる力が誘電体の向きに働き、誘電体中には\(\frac{\sigma^2}{2\varepsilon}\)[J/m\(^3\)]なる電界エネルギーが貯えられている。
コンデンサを用いて考える。
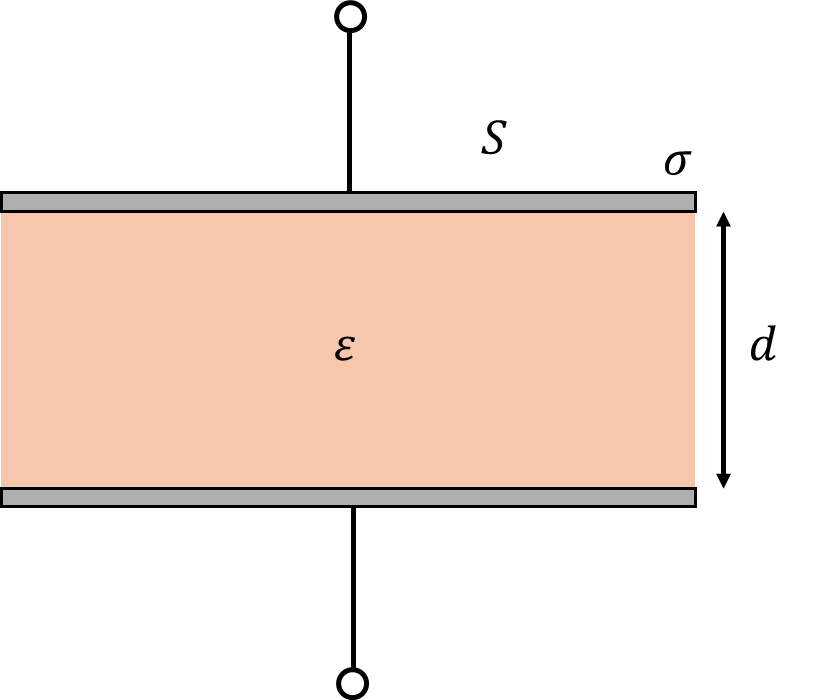
誘電体内部の電界\(E\)は、電束密度を\(D\)とすると、
\[E=\frac{D}{\varepsilon}\]
である。ここで、面電荷密度\(\sigma\)は電束密度\(D\)と等しいことから、
\[E=\frac{\sigma}{\varepsilon}\]
となる。導体(極板)に働く力\(F\)は、コンデンサの静電エネルギー\(W\)を極板間距離\(d\)で除すことで求まる。
コンデンサの静電エネルギー\(W\)は、極板間の電位差を\(V\)とすると、
\[W=\frac{1}{2}CV^2=\frac{1}{2}\frac{\varepsilon S}{d}(Ed)^2=\frac{1}{2}\frac{\varepsilon S}{d}\Big(\frac{\sigma}{\varepsilon}d\Big)^2=\frac{\sigma^2 Sd}{2\varepsilon}\]
よって、
\[F=\frac{W}{d}=\frac{\sigma^2 S}{2\varepsilon}\]
ここで、単位面積当たりの力は、\(S=1\)より
\[F=\frac{\sigma^2}{2\varepsilon}\]
また、単位体積あたりに電界に貯えられるエネルギーは、\(Sd=1\)より
\[W=\frac{\sigma^2}{2\varepsilon}\]
高調波
(2)各相における大きさが等しく、また、基本波に対して同じ位相関係をもつ高調波の存在する三相回路においては、周波数が\(3n\)倍の高調波は、各相同位相である。したがって、これらの高調波は、Y結線回路では、その各相電圧には存在するが、線間電圧には現れない。一方、\(\Delta\)結線回路では、その結線中には、大きさが\(3\)倍の高調波電圧が生じ、循環電流が流れる。
以下の図を用いて解説する。
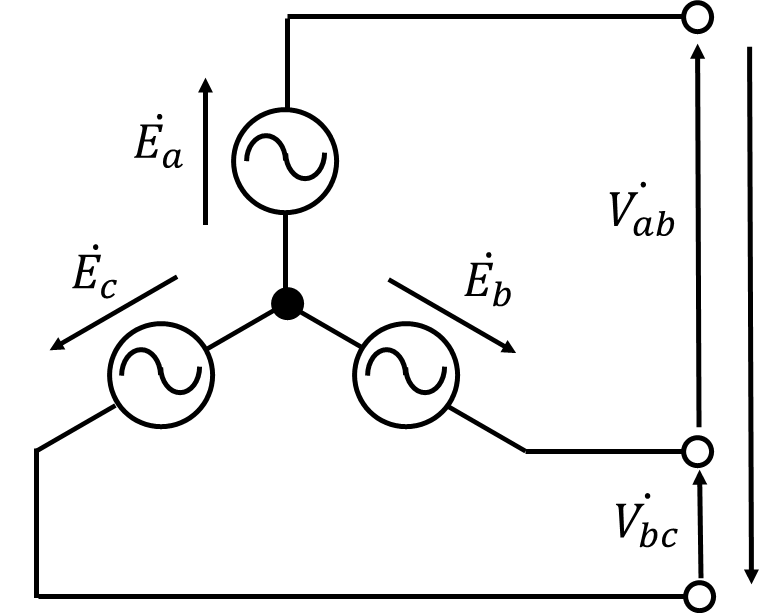
三相起電力を以下のように定義する。
\[\dot{E_a}=E\sin{\omega t}+E_3\sin{3n\omega t}\]
\[\dot{E_b}=E\sin{(\omega t-\frac{2}{3}\pi)}+E_3\sin{3n(\omega t-\frac{2}{3}\pi)}\]
\[\dot{E_c}=E\sin{(\omega t-\frac{4}{3}\pi)}+E_3\sin{3n(\omega t-\frac{4}{3}\pi)}\]
それぞれ、第一項は基本波、第二項は第\(3n\)次高調波である。上式を整理すると、
\[\dot{E_a}=E\sin{\omega t}+E_3\sin{3n\omega t}\]
\[\dot{E_b}=E\sin{(\omega t-\frac{2}{3}\pi)}+E_3\sin{3n\omega t}\]
\[\dot{E_c}=E\sin{(\omega t-\frac{4}{3}\pi)}+E_3\sin{3n\omega t}\]
ここで、\(\sin\)の引数である\(2n\pi\)や\(4n\pi\)は、もとの位相と同相であることを示す。(フェーザの位相が\(n\)周してもとの場所に戻っただけ)
線間電圧を求めると、
\[\dot{V_{ab}}=\dot{E_a}-\dot{E_b}=\sqrt{3}E\sin{\omega t+\frac{\pi}{6}}\]
\[\dot{V_{bc}}=\dot{E_b}-\dot{E_c}=\sqrt{3}E\sin{\omega t-\frac{\pi}{2}}\]
\[\dot{V_{ca}}=\dot{E_c}-\dot{E_a}=\sqrt{3}E\sin{\omega t+\frac{5}{6}\pi}\]
よって、Y結線の場合、第\(3n\)次高調波は相電圧には現れるが、線間電圧には現れない。
\(\Delta\)結線では相電圧\(=\)線間電圧となることから、高調波成分が現れる。
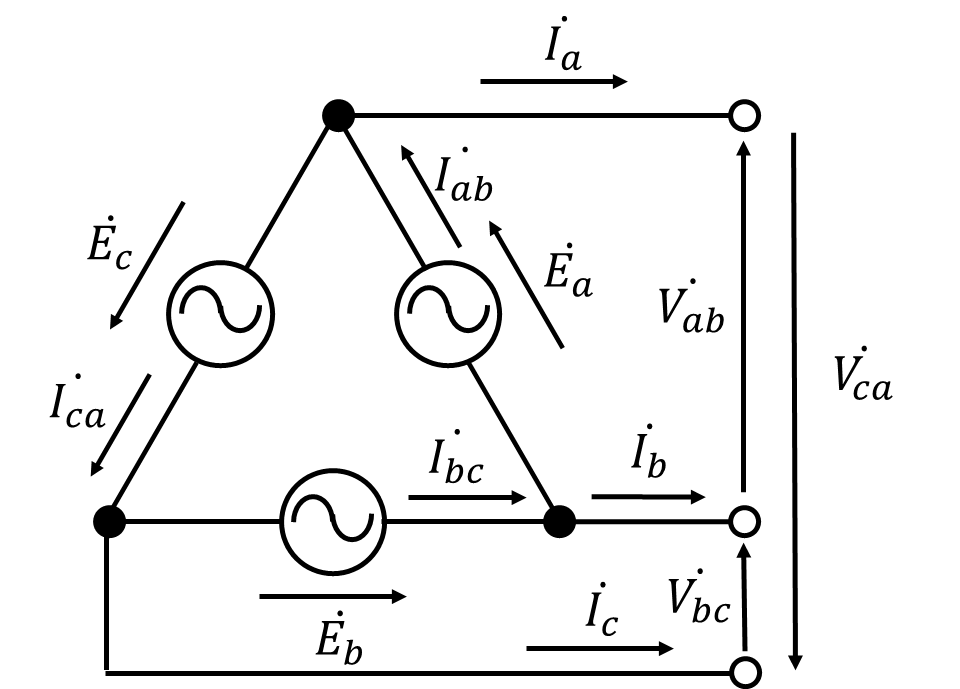
結線内の高調波電圧は、
\[E_3\sin{3n\omega t}+E_3\sin{3n\omega t}+E_3\sin{3n\omega t}=3E_3\sin{3n\omega t}\]
より、\(3\)倍の高調波電圧となる。
また、電流を以下に定義する。
\[\dot{I_{ab}}=I\sin{\omega t}+I_3\sin{3n\omega t}\]
\[\dot{I_{bc}}=I\sin{(\omega t-\frac{2}{3}\pi)}+I_3\sin{3n(\omega t-\frac{2}{3}\pi)}\]
\[\dot{I_{ca}}=I\sin{(\omega t-\frac{4}{3}\pi)}+I_3\sin{3n(\omega t-\frac{4}{3}\pi)}\]
上式を整理すると
\[\dot{I_{ab}}=I\sin{\omega t}+I_3\sin{3n\omega t}\]
\[\dot{I_{bc}}=I\sin{(\omega t-\frac{2}{3}\pi)}+I_3\sin{3n\omega t}\]
\[\dot{I_{bc}}=I\sin{(\omega t-\frac{4}{3}\pi)}+I_3\sin{3n\omega t}\]
よって、線電流は
\[\dot{I_a}=\dot{I_{ab}}-\dot{I_{ca}}=\sqrt{3}I\sin{\omega t+\frac{\pi}{6}}\]
\[\dot{I_b}=\dot{I_{bc}}-\dot{I_{ab}}=\sqrt{3}I\sin{(\omega t-\frac{\pi}{2})}\]
\[\dot{I_c}=\dot{I_{ca}}-\dot{I_{bc}}=\sqrt{3}I\sin{(\omega t+\frac{5}{6}\pi)}\]
よって、\(\Delta\)結線では線電流に高調波成分が現れず、結線内を循環することがわかる。
電気計測
(3)静電形計器は、2枚の電極の間の静電力を利用したもので、消費電力が極めて少ないから、高電圧・高インピーダンス回路の電圧測定に適し、また、周波数特性が優れているので、直流から高調波まで測定可能であり、指示は実効値を示す。
出典
昭和56年度第二種電気主任技術者筆記試験理論問3



コメント