~単相交流回路~
問題
図のように、抵抗、インダクタンス及びキャパシタンスの3素子が直列に接続されている回路に交番電圧\(\dot{E}\)(角周波数\(\omega\))を印加したとき、次の問に答えよ。

(1)流れる電流の大きさの絶対値\(|\dot{I}|\)を求め、かつ、\(|\dot{I}|\)の\(\omega\)による変化を示す図を定性的に描け。
(2)回路に消費される平均電力が、直列共振時の平均電力の\(\frac{1}{2}\)になる半電力点の角周波数を求めよ。ただし、共振角周波数を\(\omega_0\)とする。
(3)この回路の共振時の電圧拡大率\(Q\)(共振の尖鋭度)を、\(\omega_0\)及び半電力点の角周波数をもって示せ。
解答
(1)流れる電流の大きさの絶対値\(|\dot{I}|\)は
\[|\dot{I}|=\frac{E}{\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}}\]
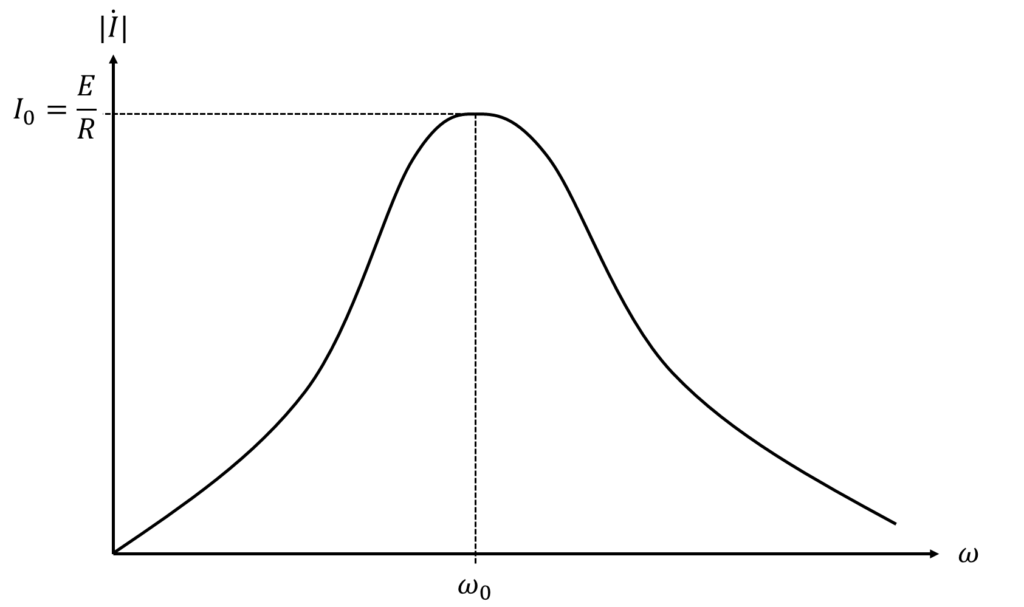
\(|\dot{I}|\)の\(\omega\)による変化を図に示す。
(2)半電力点の角周波数\(\omega_1\)、\(\omega_2\)は
\[\omega_1=-\frac{R}{2L}+\sqrt{\left(\frac{R}{2L}\right)^2+\omega_0^2}\]
\[\omega_2=\frac{R}{2L}+\sqrt{\left(\frac{R}{2L}\right)^2+\omega_0^2}\]
(3)共振時の電圧拡大率\(Q\)(共振の尖鋭度)は
\[Q=\frac{\omega_0}{\omega_2-\omega_1}\]
解説
(1)
回路のインピーダンス\(\dot{Z}\)の大きさ\(|\dot{Z}|\)は
\[|\dot{Z}|=Z=\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)}\]
であることから、\(|\dot{I}|=\frac{E}{Z}\)より
\[|\dot{I}|=\frac{E}{\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)}}\]
\(|\dot{I}|\)の\(\omega\)による変化を描くため、インピーダンスを複素数\(\dot{Z}\)で考える。
\[\dot{Z}=R+j\left(\omega L-\frac{1}{\omega C}\right)\]
よって、\(\dot{Z}\)が\(\omega\)によって変化するには虚部のみである。
\(\omega L-\frac{1}{\omega C}=0\)となるときが共振であり、\(\dot{Z}\)の虚部が\(0\)となり\(Z\)が最小となる(\(Z=R\))。このときの\(\omega\)は
\[\omega L-\frac{1}{\omega C}=0\to \omega L=\frac{1}{\omega C}\to \omega=\frac{1}{\sqrt{LC}}\]
電圧を基準ベクトルとしたときのインピーダンスのフェーザ図を示す。
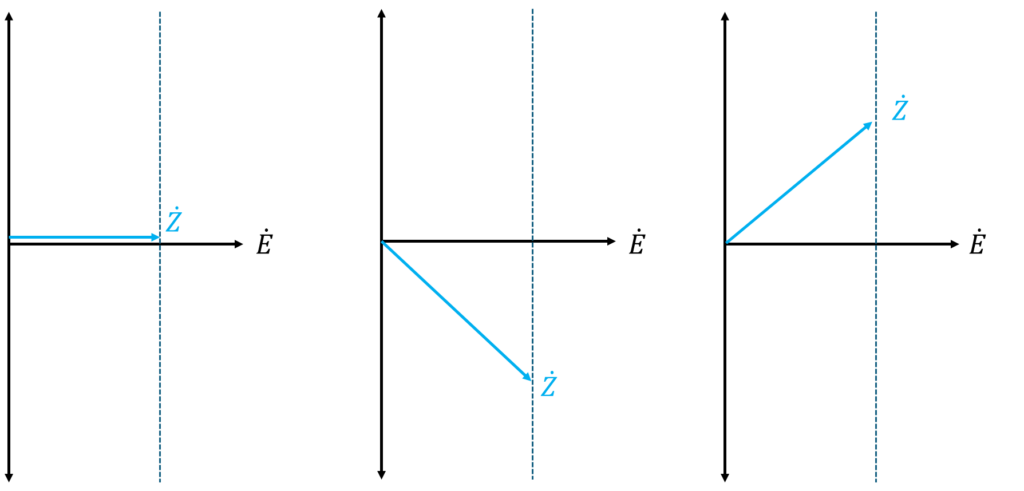
\(\omega\)が変化しても\(\dot{Z}\)の実部は変化しない(フェーザ図中の点線)。
矢印の長さが大きさに当たることから、力率100%のときインピーダンスが最小であり、\(\dot{E}\)を中心に対称に動く。
ただし、\(\omega=0\)(直流)ではコンデンサが開放と等価であることから、\(|\dot{I}|=0\)となる。
これを基に\(|\dot{I}|\)のグラフを描くと、以下のようになる。

(2)
直列共振時、流れる電流は\(I_0=\frac{E}{R}\)となる。
電流は、抵抗値が一定のとき電力の平方根に比例することから、半電力での電流\(I_{half}\)は\(\frac{1}{\sqrt{2}}\)倍となり、
\[I_{half}=\frac{I_0}{\sqrt{2}}\]
が成り立つ。これより、\(\frac{I_0}{I_{half}}=\sqrt{2}\)という関係から、半電力での角周波数を\(\omega_h\)とおくと、
\[\frac{I_0}{I_{half}}=\sqrt{2}=\frac{\frac{E}{R}}{\frac{E}{\sqrt{R^2+\left(\omega_h L-\frac{1}{\omega_h C}\right)^2}}}=\frac{\sqrt{R^2+\left(\omega_h L-\frac{1}{\omega_h C}\right)^2}}{R}\]
\[2R^2=R^2+\left(\omega_h L-\frac{1}{\omega_h C}\right)^2\to R^2=\left(\omega_h L-\frac{1}{\omega_h C}\right)^2\]
\[\omega_h L-\frac{1}{\omega_h C}=\pm R\]
よって、\(\omega_h\)は2つ存在する。
\(\omega_1\)
\(\omega_h L<\frac{1}{\omega_h C}\)のときの\(\omega_h\)を\(\omega_1\)とすると
\[\omega_1 L-\frac{1}{\omega_1 C}=-R\to \omega_1^2LC-1=-\omega_1CR\]
\[\omega_1^2+\frac{R}{L}\omega_1-\frac{1}{LC}=0\]
\(\frac{1}{\sqrt{LC}}=\omega_0\)より、
\[\omega_1^2+\frac{R}{L}\omega_1-\omega_0^2=0\]
\[\omega_1=\frac{-\frac{R}{L}\pm \sqrt{\left(\frac{R}{L}\right)^2+4\omega_0^2}}{2}\]
\(\omega\)は正の値であることから、
\[\omega_1=\frac{-\frac{R}{L}+ \sqrt{\left(\frac{R}{L}\right)^2+4\omega_0^2}}{2}=-\frac{R}{2L}+\sqrt{\left(\frac{R}{2L}\right)^2+\omega_0^2}\]
\(\omega_2\)
\(\omega_h L>\frac{1}{\omega_h C}\)のときの\(\omega_h\)を\(\omega_2\)とすると
\[\omega_2 L-\frac{1}{\omega_2 C}=R\to \omega_2^2LC-1=\omega_2CR\]
\[\omega_2^2-\frac{R}{L}\omega_2-\omega_0^2=0\]
\[\omega_2=\frac{\frac{R}{L}\pm \sqrt{\left(\frac{R}{L}\right)^2+4\omega_0^2}}{2}\]
\(\omega\)は正の値であることから、
\[\omega_2=\frac{\frac{R}{L}+ \sqrt{\left(\frac{R}{L}\right)^2+4\omega_0^2}}{2}=\frac{R}{2L}+\sqrt{\left(\frac{R}{2L}\right)^2+\omega_0^2}\]
(3)
電圧拡大率(尖鋭度)\(Q\)は、回路の鋭さを表している。
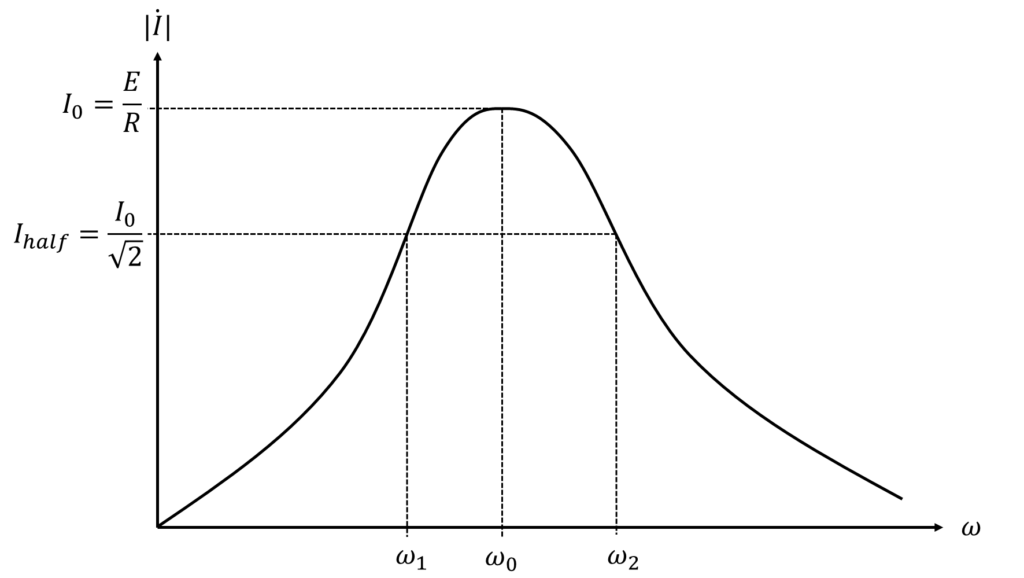
\[Q=\frac{\omega_0}{\omega_2-\omega_1}\]
と定義される。
(2)より、\(\omega_2-\omega_1=\frac{R}{L}\)であり、
\[Q=\frac{\omega_0}{\omega_2-\omega_1}=\frac{\omega_0L}{R}=\frac{1}{\omega_0CR}\]
とも表せる。
\(\omega=\omega_0\)のとき、\(\omega_0L=\frac{1}{\omega_0C}\)となることに留意(直列共振)。
出典
昭和55年度第二種電気主任技術者筆記試験理論問2



コメント