~同心導体球の静電容量、抵抗~
問題
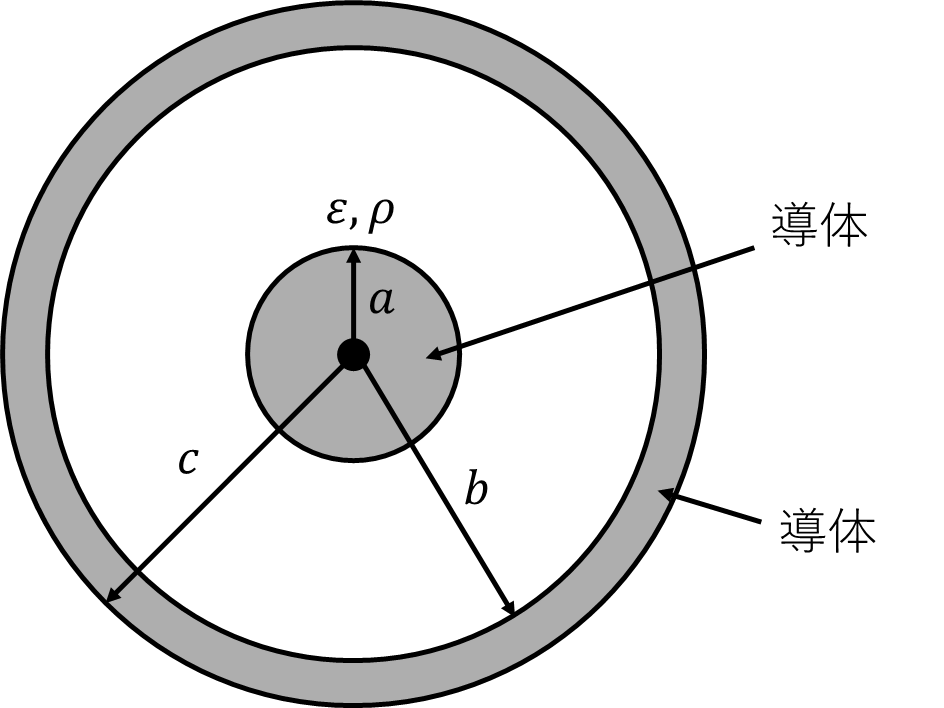
図に示すような2個の同心導体球があり、内球導体の半径を\(a\)[m]、外球導体の内半径を\(b\)[m]、外半径を\(c\)[m]とする。両導体球間に誘電率\(\varepsilon\)[F/m]、抵抗率\(\rho\)[Ω・m]の物質を満たしたとき、両導体球間の静電容量及び抵抗を求めよ。
解答
両導体球間の静電容量は
\[C=4\pi \varepsilon\left(\frac{ab}{b-a}\right)\]
両導体球間の抵抗は
\[R=\frac{\rho}{4\pi}\left(\frac{b-a}{ab}\right)\]
解説
導体球の中心から半径\(r\)の閉局面を仮定する。
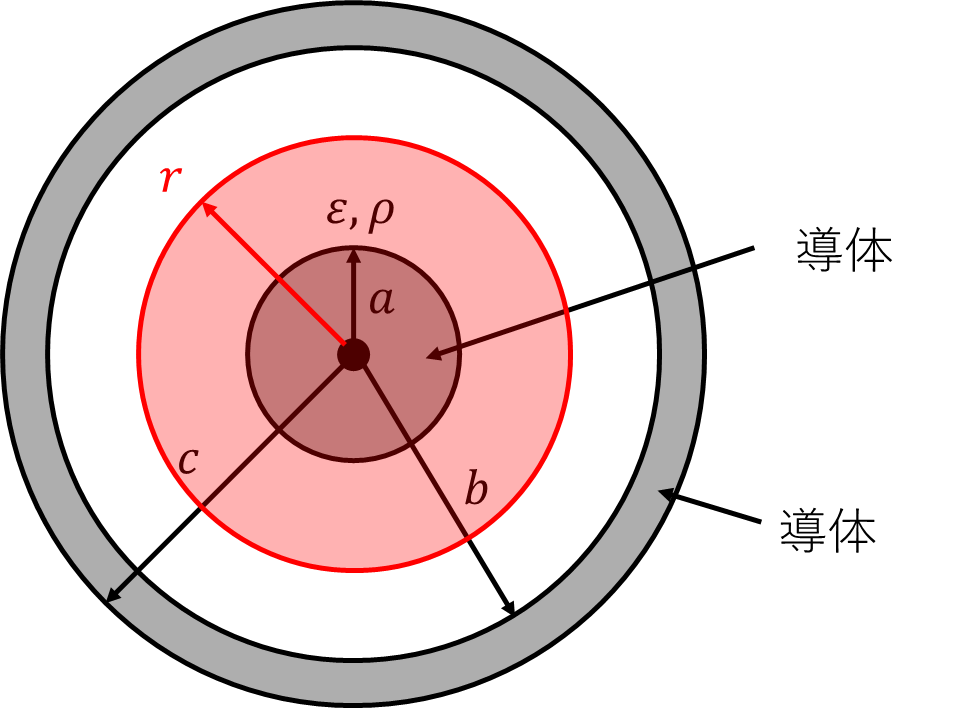
内球に\(Q\)[C]、外球に\(-Q\)[C]の電荷をもっているとする。
このとき、\(r\)での電界\(E\)は、ガウスの法則より
\[\oint_s{E\cdot ds=\frac{Q}{\varepsilon}}\to 4\pi r^2E=\frac{Q}{\varepsilon}\to E=\frac{Q}{4\pi \varepsilon r^2}\]
これから内球と外球の電位差を求めると、
\[V=-\int^{a}_{b}{Edr}=\frac{Q}{4\pi \varepsilon}\left(\frac{1}{a}-\frac{1}{b}\right)\]
よって、静電容量は
\[C=\frac{Q}{V}=\frac{Q}{\frac{Q}{4\pi \varepsilon}\left(\frac{1}{a}-\frac{1}{b}\right)}=\frac{4\pi \varepsilon}{\frac{1}{a}-\frac{1}{b}}=4\pi \varepsilon\left(\frac{ab}{b-a}\right)\]
次に抵抗を求める。
導体の長さ\(l\)、断面積を\(S\)とすると、\(R=\rho\frac{l}{S}\)より\(r\)における微小距離\(dr\)の抵抗\(dR\)は
\[dR=\rho\frac{dr}{4\pi r^2}\]
導体球間の抵抗は\(dR\)を\(a\)から\(b\)まで\(r\)について積分することで求められる。
\[R=\int^{b}_{a}{\rho\frac{dr}{4\pi r^2}}=\frac{\rho}{4\pi}\int^{b}_{a}{\frac
{1}{r^2}dr}=-\frac{\rho}{4\pi}\left(\frac{1}{b}-\frac{1}{a}\right)=\frac{\rho}{4\pi}\left(\frac{b-a}{ab}\right)\]
別解として、\(CR=\varepsilon \rho\)が成り立つことを利用して解くのもよい。
まず\(R\)を上記の手順で求めた後に、\(C=\frac{\varepsilon \rho}{R}\)を用いて解く方がスマートなのかな。
\(CR=\varepsilon \rho\)が成り立つ理由を解説します。
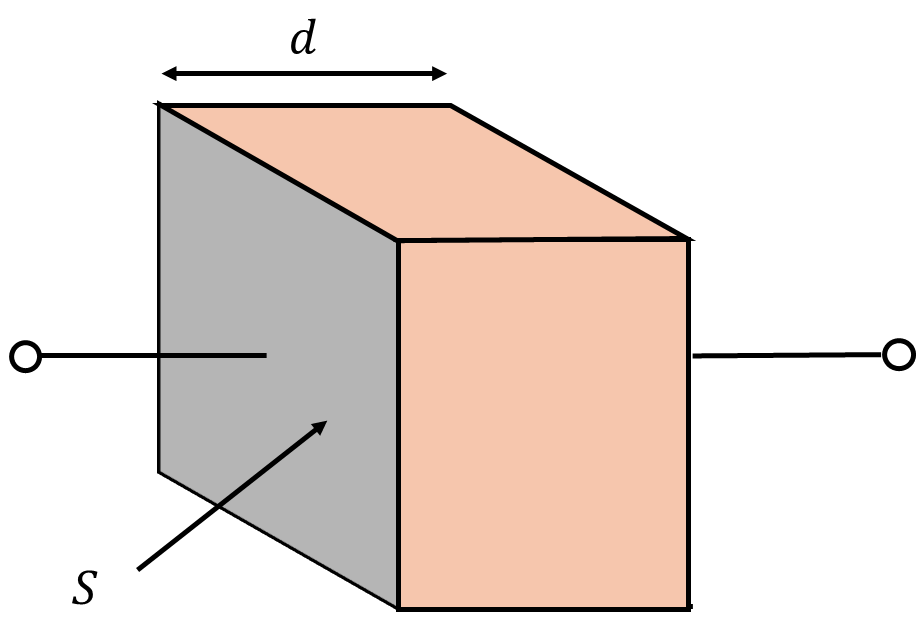
図のような平行平板電極を考えます。
静電容量は\(C=\frac{\varepsilon S}{d}\)、抵抗は\(R=\rho\frac{d}{S}\)ですね。
よって、\(RC=\varepsilon \rho\)です。カンタンですネ
この関係は電極形状に関係しません。なので同心導体球間でも適用できる訳なんですね。
出典
昭和55年度第二種電気主任技術者筆記試験理論問1




コメント