~配電線路の電力損失~
問題
給電点における年間最大負荷電流\(100\)[A]、配電距離\(1\)[km]で、直径\(5\)[mm]の硬銅線(長さ\(1\)[m]、断面積\(1\)[mm\(^2\)]の抵抗は\(\frac{1}{55}\)[Ω]とする)を使用した三相3線式\(6\)[kV]高圧配電線路がある。線路中の年間損失電力量は、何キロワット時となるか。ただし、負荷は、全配電線路にわたり平等に分布し、かつ、同一の負荷曲線を有するものとし、年損失係数を\(0.3\)とする。
解答
\(24300\)[kW・h]
解説
問題の条件を図に示す。
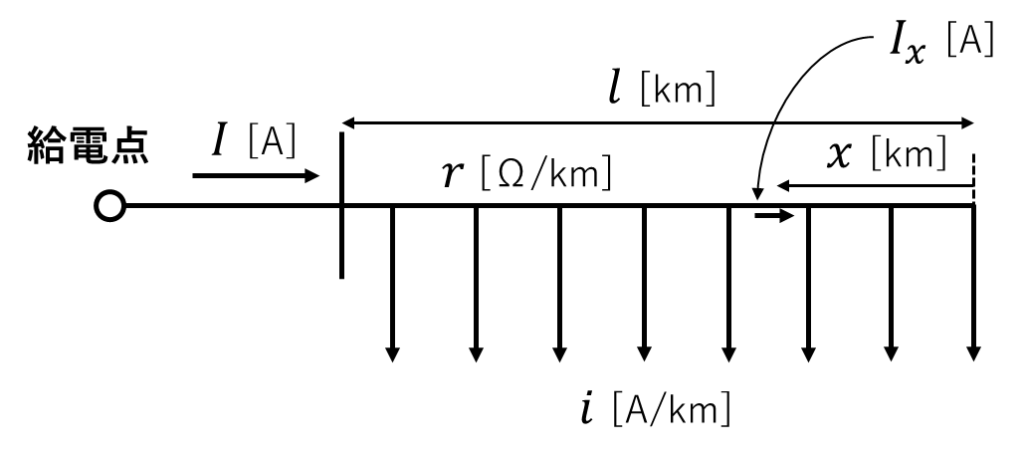
ここで、変数は\(x\)、\(I_x\)である。
負荷密度\(i\)は
\[i=\frac{I}{l}\]
負荷端から\(x\)[km]の地点における電流を\(I_x\)とすると、
\[I_x=ix=\frac{x}{l}I\]
よって、電流は給電点から負荷端に向かうにつれて直線的に減少する。
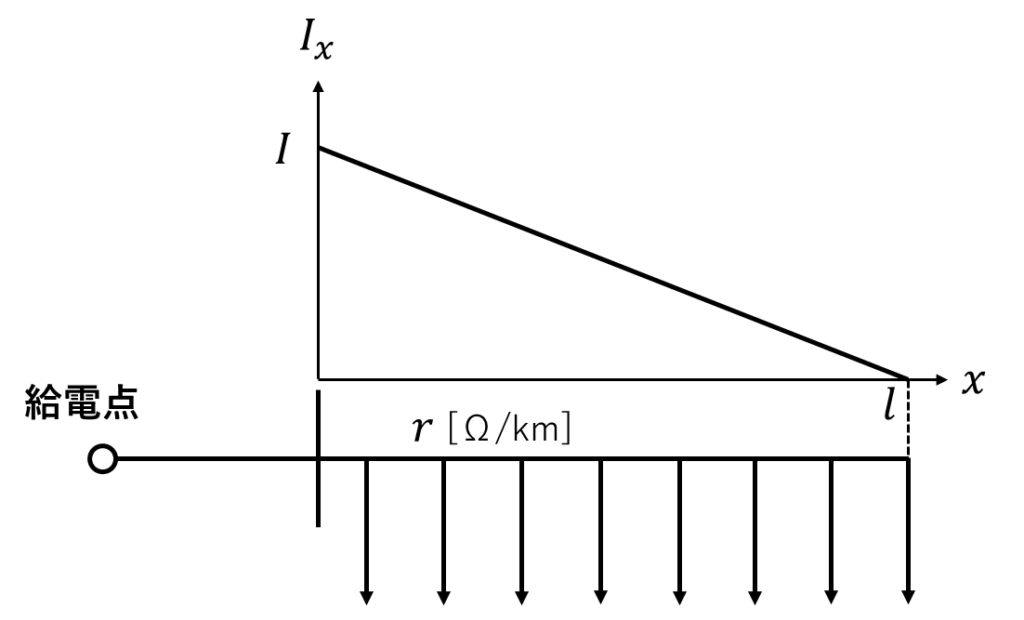
一線あたりの抵抗を\(r\)[Ω/km]とすると、電力損失\(P_l\)は微小距離\(dx\)での電力損失\(dp_l\)を負荷端から給電点まで積分することで求められる。
\[P_l=\int^{l}_{0}{dp_l}=\int^{l}_{0}{3I_x^2rdx}=\int^{l}_{0}{3\left(\frac{x}{l}I\right)^2rdx}\]
\[=\frac{3I^2r}{l^2}\int^{l}_{0}{x^2dx}=\frac{3I^2r}{l^2}[\frac{1}{3}x^3]^{l}_{0}=I^2rl[W]\]
ここで、\(r\)は距離に比例し、断面積に反比例することから、比例計算して
\[r=\frac{1}{55}\times \frac{\frac{1000}{\pi\left(\frac{5}{2}\right)^2}}{\frac{1}{1}}=0.92599[Ω]\]
年間損失係数は\(0.3\)であることから、1年間(8760時間)の電力損失\(W\)は
\[W=I^2rl\times 0.3\times 1\times 8760\times 10^{-3}\]
\[=100^2\times 0.92599\times 0.3\times 1\times 8760\times 10^{-3}\]
\[=24335.017\to 24300[kW・h]\]
ちなみに、年損失係数は以下で定義される。
\[損失係数=\frac{ある期間の電流の二乗の平均}{その期間の最大電流の二乗}\]
出典
昭和55年度第二種電気主任技術者筆記試験送配電問2



コメント