~送電線の反射波~
問題
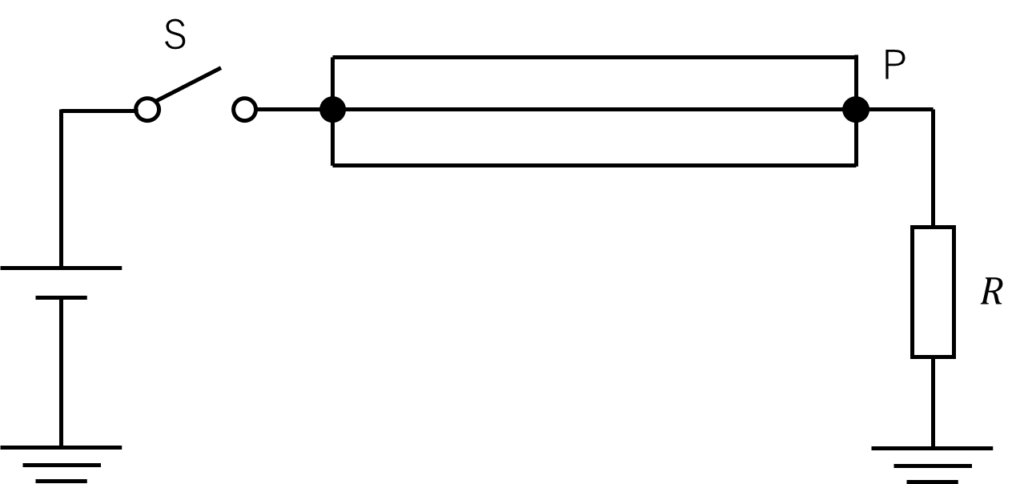
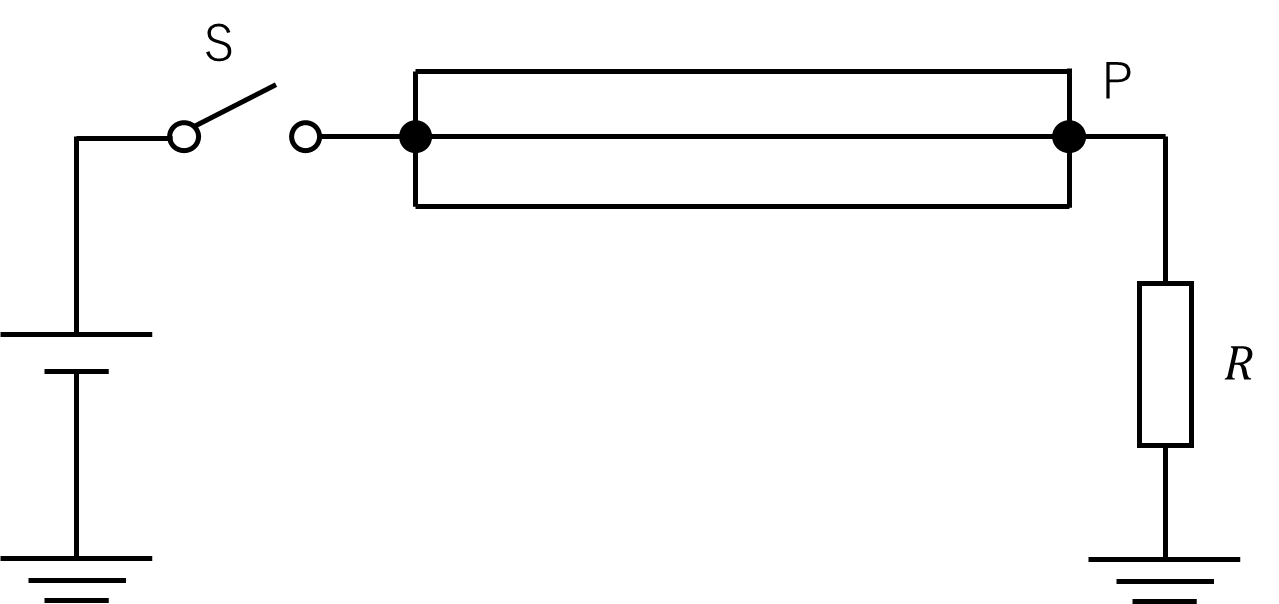
各線の自己サージインピーダンス及び相互サージインピーダンスがそれぞれ\(Z\)及び\(Z_m\)である三相1回線送電線において、図のように3線を一括し、しゃ断器Sを閉じて電圧を加えた場合、終端Pで反射波を生じないための条件を求めよ。
解答
\[R=\frac{Z+2Z_m}{3}\]
解説
まず、3線を一括したサージインピーダンス\(Z_0\)を求める。
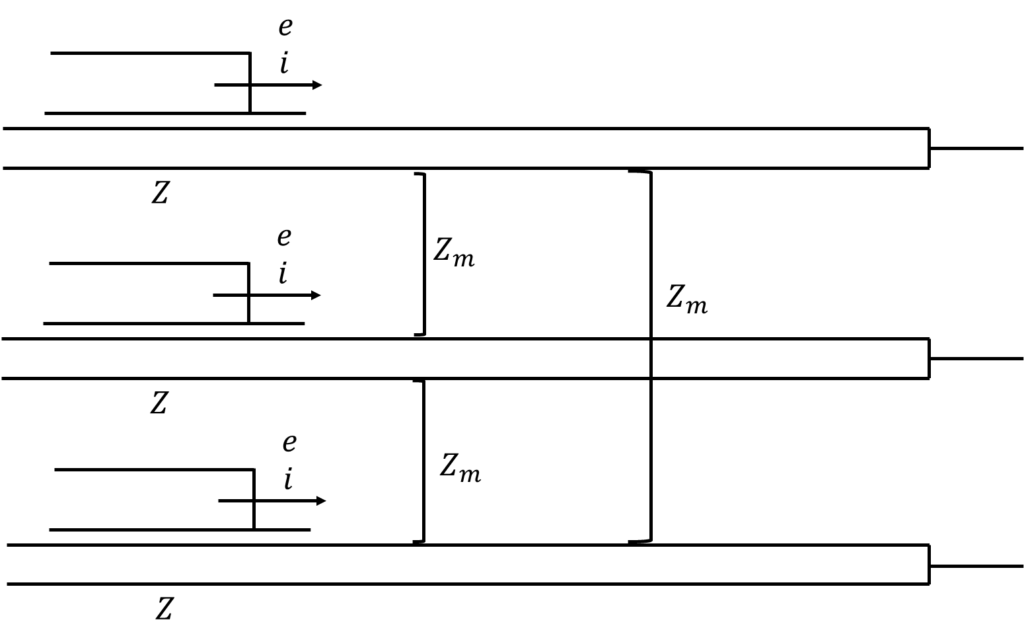
\[e=iZ+iZ_m+iZ_m=i(Z+2Z_m)\]
第一項は自己サージインピーダンスによる電圧、第ニ項・第三項は他の2線の相互サージインピーダンスによる電圧である。
ここで、1線あたりのサージインピーダンス\(Z_1\)は
\[Z_1=\frac{e}{i}=\frac{i(Z+2Z_m)}{i}=Z+2Z_m\]
よって、送電線全体のサージインピーダンス\(Z_0\)は、3線が並列になっていることから
\[Z_0=\frac{Z_1}{3}=\frac{Z+2Z_m}{3}\]
となる。これをもとに、図を描き換える。
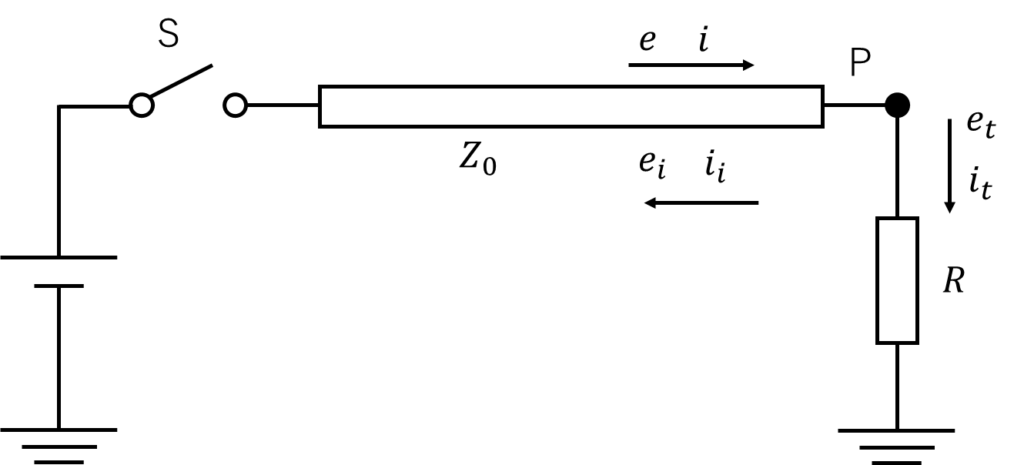
ここで、入射波\(e i\)、反射波\(e_i i_i\)、透過波\(e_t i_t\)としている。図より、以下の式が成り立つ。
\[e+e_i=e_t i+i_i=i_t\]
\[i=\frac{e}{Z_0} i_i=-\frac{e_i}{Z_0} i_t=\frac{e_t}{R}\]
電流式に着目し、
\[\frac{e}{Z_0}-\frac{e_i}{Z_0}=\frac{e_t}{R}\to \frac{e-e_i}{Z_0}=\frac{e_t}{R}\]
\(e_t=e+e_i\)より、
\[\frac{e-e_i}{Z_0}=\frac{e+e_i}{R}\to e\left(\frac{1}{Z_0}-\frac{1}{R}\right)=e_i\left(\frac{1}{Z_0}+\frac{1}{R}\right)\]
\(e_i\)について解くと
\[e_i=\frac{\frac{1}{Z_0}-\frac{1}{R}}{\frac{1}{Z_0}+\frac{1}{R}}e=\frac{R-Z_0}{R+Z_0}e\]
よって、\(R=Z_0\)のときに反射波\(e_i\)が\(0\)となる。
\[R=Z_0=\frac{Z+2Z_m}{3}\]
\(R\)が3線を一括したときのサージインピーダンスに等しいとき、反射波を生じなくなる。
これはインピーダンスマッチングの考え方であり、入力インピーダンスと負荷インピーダンスの値が等しくなると反射が生じず、負荷で最大電力を得られる。
出典
昭和55年度第二種電気主任技術者筆記試験送配電問1


コメント